多因子模型再述
APT思想再述
一个证券i收益率R发生了变化,背后的原因分为两大类:公共因素(系统性)的和公司特有因素(非系统性)。
比如今年美国的牛奶生产企业,最近每天要倾倒40万加仑牛奶,这显然会影响牛奶企业的收益率。奶企业的今年的营收状况可以归因与两大方面,一方面可以归因于宏观因素(新冠疫情);另一方面可以归因于自身因素(管理不善、运气不好)。那么用模型表述这个思想:
\[ r_{it}=E\left(r_{it}\right)+\beta_{i} F_t+e_{it} \]
这里的\(E(r_{it})\)是奶牛企业历史收益率的均值,\(F_t\)是公共风险因素偏离历史期望收益,\(\beta_i\) 代表了i企业对F这种公共风险因素的敏感度(载荷)
显然\(\beta_i\)越大,意味着i这家企业对F公共风险因素的敏感度越大
对于单个企业而言,\(e_{it}\)就是这个企业的特有风险(个体风险)
从现实中来考虑,很自然的我们可以把一个公共风险因素扩展到两个甚至多个
\[\mathrm{E}\left[R_{i}\right]=\beta_{i}^{\prime} \lambda, \quad i=1,2, \cdots, N\]
模型的左边\(R_i\)代表了股票i的超额收益,减去了\(r_f\),注意这里没有\(\alpha_i\)
\(\beta_i^{\prime}\)代表了第i个股票的\(K\times1\)阶的因子暴露(factor-loading,风险敏感程度)
\(\lambda\)为\(K\times1\)阶的因子收益均值向量
\[r_{P}=E\left(r_{p}\right)+\beta_{P} F+e_{P}\]
\(\beta_{P}=\sum w_{i} \beta_{i}\)是n个证券\(\beta_i\)的加权平均
基于单个资产不相关假设:\(e_{p}=\sum w_{i} e_i\)为该组合的非系统风险部分
投资组合p的方差为:
\[\sigma_{p}^{2}=\beta_{p}^{2} \sigma_{F}^{2}+\sigma^{2}\left(e_{p}\right)\]
\[\sigma^{2}\left(e_{p}\right)=\left(\sum w_{i} e_{i}\right) \quad \text { 的方差 }=\sum w_{i}^{2} \sigma^{2}\left(e_{i}\right)\]
\[如果进行等权重或者接近等权重投资\left(\frac{1}{N}\right)^{2} \times N \times \sigma_{i}^{2}=\frac{\sigma_{i}^{2}}{N}=0\]
说了这么多,本质上就是告诉大家非系统性风险被分散光了
\[两个风险模型中就没有残差项了: r_{P}=E\left(r_{P}\right)+\beta_{1} F_{1}+\beta_{2} F_{2}\]
套利组合的特性
完善的证券市场不允许任何套利机会存在
1.初始投资为零,即对投资组合\(P=\left(w_{1}, \cdots, w_{N}\right) \text { 有 } \sum_{i=1}^{N} w_{i}=0\)
2. 投资组合的风险为零,风险分为因子暴露风险和非因子暴露风险(特质)对于暴露风险,我们可以通过投资组合分配,将其风险因子载荷做成0
\[\sum_{i=1}^{N} \beta_{i}^{(k)} w_{i}=0\]
对于特质性风险,我们可以进行N投资个体,趋近于无穷大的方式进行分散
3.投资组合的的盈利为正。\(\text { 即 } \sum_{i=1}^{N} w_{i} r_{i}=0, \text { 结合前两条, } \text { 有 } \sum_{i=1}^{N} w_{i} \alpha_{i}=0\)
实证多因子模型思路
因子模型希望回答的是:股票的(超额)收益率期望在截面上(即不同的股票之间)为什么会有差异?
为什么在同一个时间有的资产收益率高,有的资产收益率低?
这周,为什么为什么有的股票其收益率远高于另一些股票?为什么有一些资产组合的收益率远高于另一些资产?
高度抽象的一个模型
\[\mathrm{E}\left[R_{i}\right]=\beta_{i}^{\prime} \lambda, \quad i=1,2, \cdots, N\]
根据模型如果资产i在因子上的暴露越高\(\beta_i\)越大,它的期望收益\(E(R_i)\)越大
模型的因子代表了我们对资产收益率的认知(理解)。一旦这种认知给定后,资产的预期收益率就完全由它在这些因子上的暴露决定了 。
暴露高,预期收益率就高;预期收益率是因子暴露的线性函数。 怎样找到最好的因子结构 —— 即哪些因子使得个股在截面上的预期收益率区分度高 —— 就是因子模型研究的问题。
图示,一个风险因子
在同一个时间点上,我们有许多资产(资产组合),假设这里我们只有一个风险暴露因子,那么不同资产的回报率的差异,就有该风险因子所解释。
虽然说这些点离这条线有上有下,但是平均而言,这些点距离直线的距离在统计意义上应该和0没有差异。
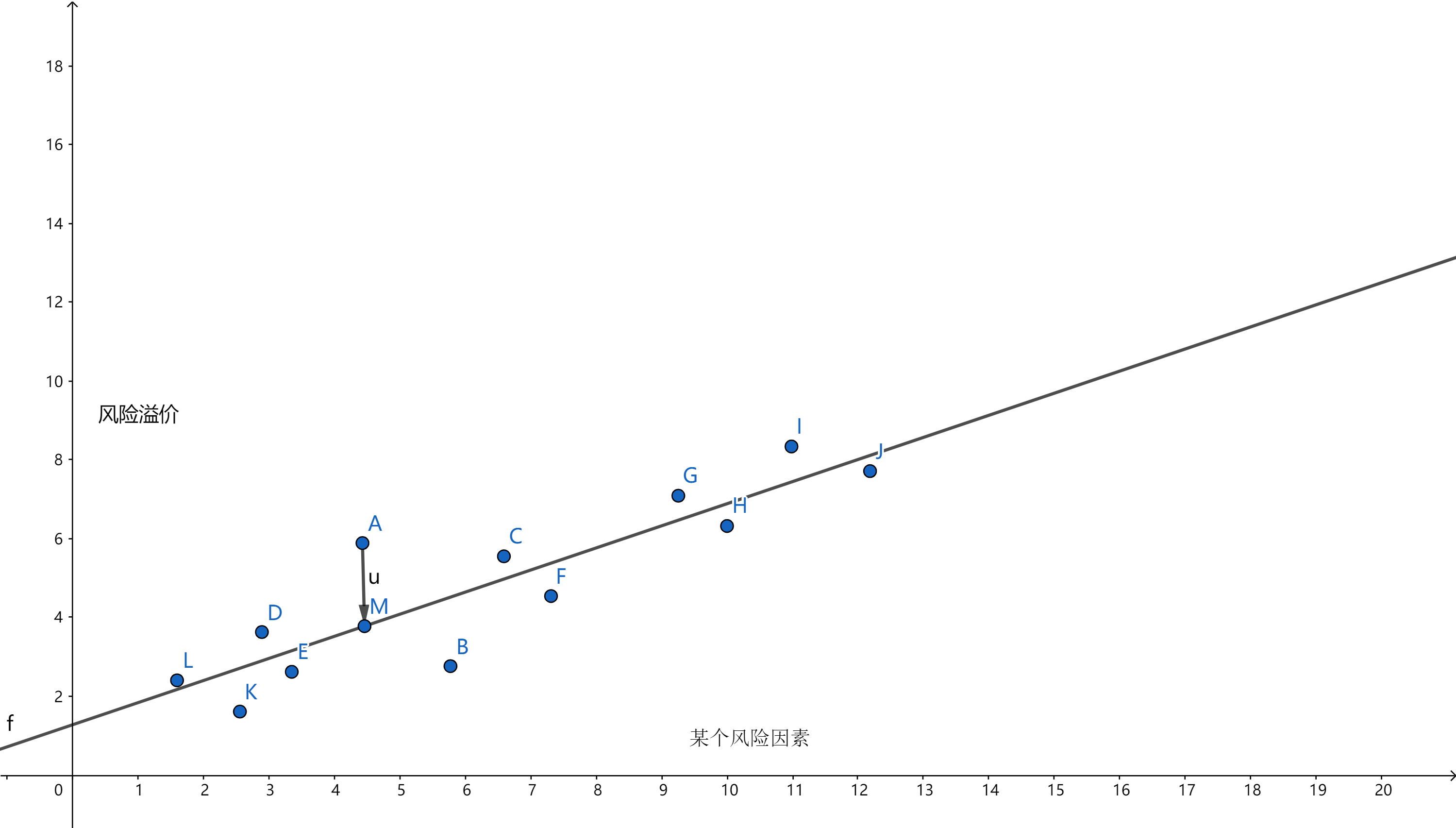
如果多于两个风险因子,那么就没有办法画二维平面图了。这些点(资产)也会距离一个风险暴露“平面”有距离,但平均而言,如果模型够好,这个距离应该和0没有显著差异。
对于一个截面估计模型而言
\[\mathrm{E}\left[R_{i}\right]=\beta_{i}^{\prime} \lambda+\alpha_{i}\]
\(\alpha_i\)代表的定价错误,要证明的就是如果模型是好模型,\(\alpha_i\)不应该显著异于0
所谓好模型——选出来的风险因子能够较好的解释个股截面预期收益率的差别
多因子模型思路
选出风险,计算个股(资产组合)在这些风险因子上的暴露(载荷)\(\beta\)
在截面上找到个股(资产组合)(超额)收益率均值和载荷\(\beta\)的线性拟合关系
检验第二步里错误定价的截距项,在统计意义上是否显著异于0
无论我们用什么因子(基本面因子、宏观经济因子、技术面因子);无论在确定截面关系时我们采用时序回归还是截面回归;对多因子模型的最终评判都转化成一个核心问题 —— 这些 alpha 联合起来是否在统计上为零。
具体实例,我们可以随便在CAPM模型的基础上增加一个因子,比如我们增加一个CPI的变化率作为因子,测试截面alpha是否显著异于0
具体实例
pacman::p_load(tidyquant,tidyverse,timetk,Tushare,DT,anytime)
api <- pro_api(token = '5adce34e8c81bf7085828754a8e09590c3630032d0f61aad6483eaaa')
bar <- pro_bar(token = '5adce34e8c81bf7085828754a8e09590c3630032d0f61aad6483eaaa')
cpi <- api(api_name = "cn_cpi",start_m='201401', end_m='202004')
cpi_m <- as_tibble(cpi) %>% select(month , nt_yoy) %>%
mutate(month = anydate(month)) %>%
mutate(year = year(month),month=month(month))
# 选择一个同比cpi作为风险因子
zz500 <- api(api_name = 'index_daily',ts_code='000905.SH',start_date="20140101",
end_date='20200407')
pingan <- bar(ts_code='601318.SH',start_date="20140101",
end_date='20200407',adj="qfq")
ghzq <- bar(ts_code='000750.SZ',start_date="20140101",
end_date='20200407',adj="qfq")
dfyl <- bar(ts_code='002310.SZ',start_date="20140101",
end_date='20200407',adj="qfq")
sdgf <- bar(ts_code='600626.SH',start_date="20140101",
end_date='20200407',adj="qfq")
hs300 <- api(api_name = 'index_daily',ts_code = '000300.SH',
start_date='20140101', end_date = '20200407')
l <- list(zz500,pingan,ghzq,dfyl,sdgf,hs300)
month_ret <- function(x) {
name = x$ts_code[1]
df = x %>% dplyr::mutate(trade_date = as.Date(trade_date,format="%Y%m%d"))
res = df %>% tq_transmute(select = close,
mutate_fun = periodReturn,
period = 'monthly',
col_rename = name)
return(res)
}
a <- map(l,month_ret)
df <- a[[4]] %>% left_join(a[[2]]) %>% left_join(a[[1]]) %>%
left_join(a[[3]]) %>% left_join(a[[6]]) %>%
rename(rm=`000300.SH`) %>% na.omit() %>%
mutate(year = year(trade_date),month = month(trade_date)) %>% select(-trade_date)
df <- df %>% left_join(cpi_m,by=c("year","month"))
df %>% datatable()mod <- list()
for (i in colnames(df)[1:4]) {
mod[[i]] = lm(df[[i]]~rm+nt_yoy,data=df)
}
int <- c()
for (i in seq(1,length(mod))) {
res = as.numeric((mod[[i]])$coefficients[1])
int <- append(int ,res)
}
t.test(int,mu = 0)##
## One Sample t-test
##
## data: int
## t = 0.13379, df = 3, p-value = 0.902
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
## -0.04346892 0.04728416
## sample estimates:
## mean of x
## 0.001907622第十三章练习题
资本市场中有两个可观测的因子\(\tilde{f}_{1}\)和\(\tilde{f}_2\)会影响资产收益率,现已知两因子相互独立,且\(E(\tilde{f_1})=0,E(\tilde{f_2})=0.02\),假设存在以下三种资产,其与风险因子的关系如下
\[\tilde{r}_1 =\alpha_1 +0.5\tilde{f}_1+\tilde{f}_2 \]
\[\tilde{r}_2 =\alpha_2 +0.4\tilde{f}_1+0.8\tilde{f}_2 \]
\[\tilde{r}_3 =\alpha_3 +0.8\tilde{f}_1+0.4\tilde{f}_2 \]
其中\(\alpha_1,\alpha_2,\alpha_3\)未知,若无风险利率\(r_f =0.02\),因子1和2的期望回报率为0.04
请在不利用APT结论的前提下,仿照APT推导过程,计算在资产市场不存在套利机会时,三种资产的期望收益率
首先构建一个风险暴露因子的载荷都为0的投资组合满足以下条件
\[w_1 + w_2+w_3 = 1\]
\[0.5\times w_1 + 0.4\times w_2+0.8\times w_3=0\]
\[w_1+0.8\times w_2 + 0.4 \times w_3 =0\]
那么这样的投资组合,由于风险因子前面的系数都是0,因此这样的投资组合的期望收益为\(r_f\)
其次构建\(\tilde{f}_2\)因子载荷为0的组合
\[w_1 + w_2+w_3 = 1\]
\[0.5\times w_1 + 0.4\times w_2+0.8\times w_3=1\]
\[w_1+0.8\times w_2 + 0.4 \times w_3 =0\]
由于题目说\(E(\tilde{f}_1)=0\),我构建的又是\(\tilde{f}_2\)因子载荷为0的组合,那么该组合的期望收益率也为\(r_f\)
接下来。无套利定价的含义是:首先构建一个投资组合,其头寸为0,也就是个各个资产权重之和为0。
其次,这个新建的组合没有风险暴露,即各个风险因子的载荷为0。
第三,如果不存在套利机会,那么我们构建的这个投资组合,其期望收益应该为0,因为我们没有出钱,头寸是0。
\[w_1 + w_2+w_3 = 0\]
\[0.5\times w_1 + 0.4\times w_2+0.8\times w_3=0\]
\[w_1+0.8\times w_2 + 0.4 \times w_3 =0\]
我用R来接矩阵吧
a <- matrix(c(1,1,1,0.5,0.4,0.8,1,0.8,0.4),nrow = 3,byrow = T)
b <- c(1,0,0)
solve(a,b)## [1] -4 5 0# 第一种组合下是w1=-4,w2=5,w3=0
a <- matrix(c(1,1,1,0.5,0.4,0.8,1,0.8,0.4),nrow = 3,byrow = T)
b <- c(1,1,0)
solve(a,b)## [1] -6.666667e-01 5.551115e-16 1.666667e+00# 第二种情况下是w1=-0.67,w2=0,w3=1.67因此我们有第一种情况下的投资组合的期望收益等于第二种情况下投资组合的期望收益
\[5\alpha_2-4\alpha_1=-0.67\alpha_1+1.67\alpha_3\]
\[3.33\alpha_1 = 5\alpha_2-1.67\alpha_3 ----(a)\]
根据无套利定价思想,我们可以进行简化,得到
\[w_3(2\alpha_1-3\alpha_2+\alpha_3)=0 ----- (b)\]
上面公式对于任意的w3应该都成立,因此要求\(2\alpha_1-3\alpha_2+\alpha_3=0\)必须满足。
将(a)带入(b),可以得到,确实(b)式得以满足。因此满足套利定价模型的三点要求,三个资产被合理定价,因此如果题目中的资产左边是减去了无风险资产\(r_f\)的风险溢价收益率的话,那么我们应该有
\[\alpha_1=\alpha_2=\alpha_3=0\]