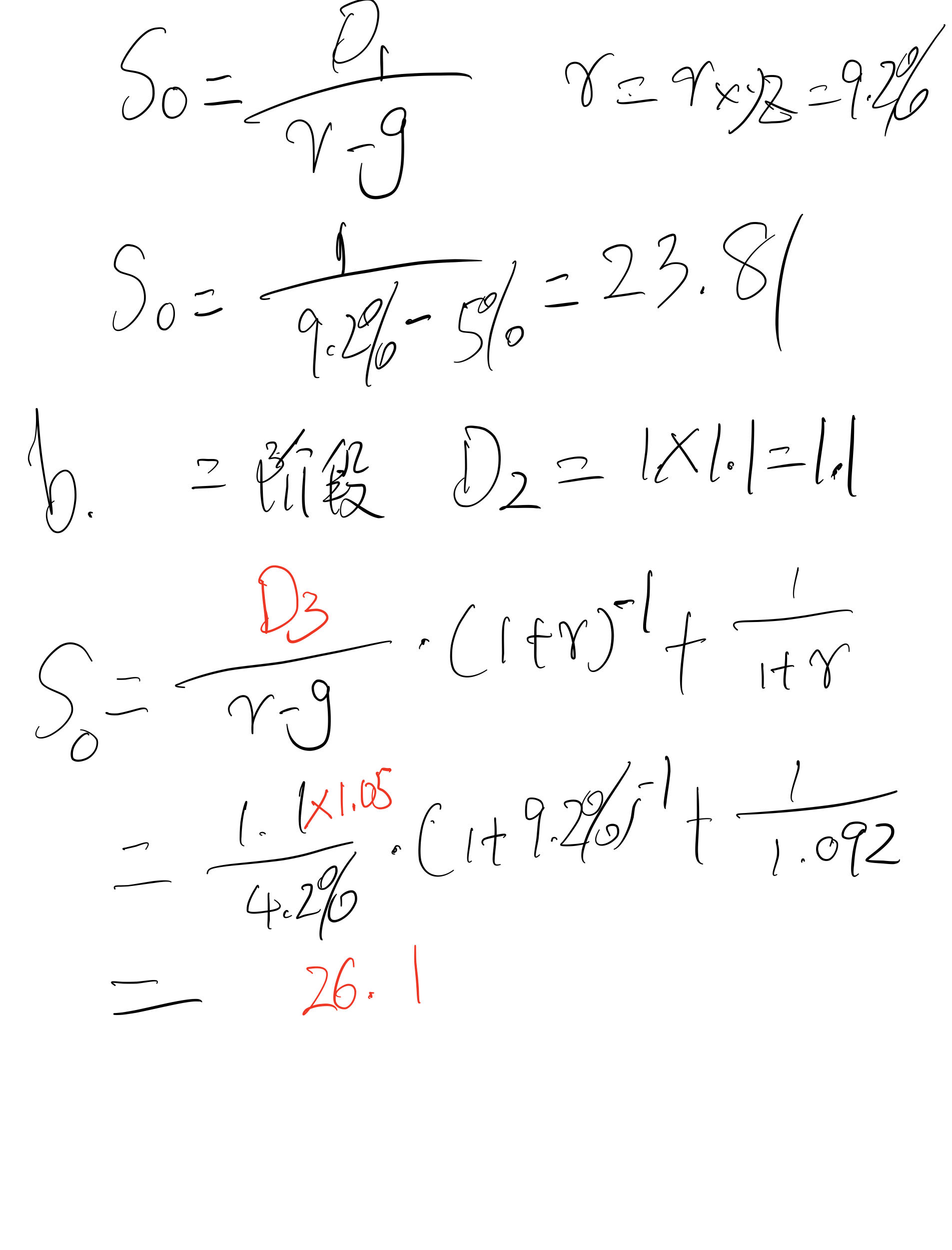第七章练习题

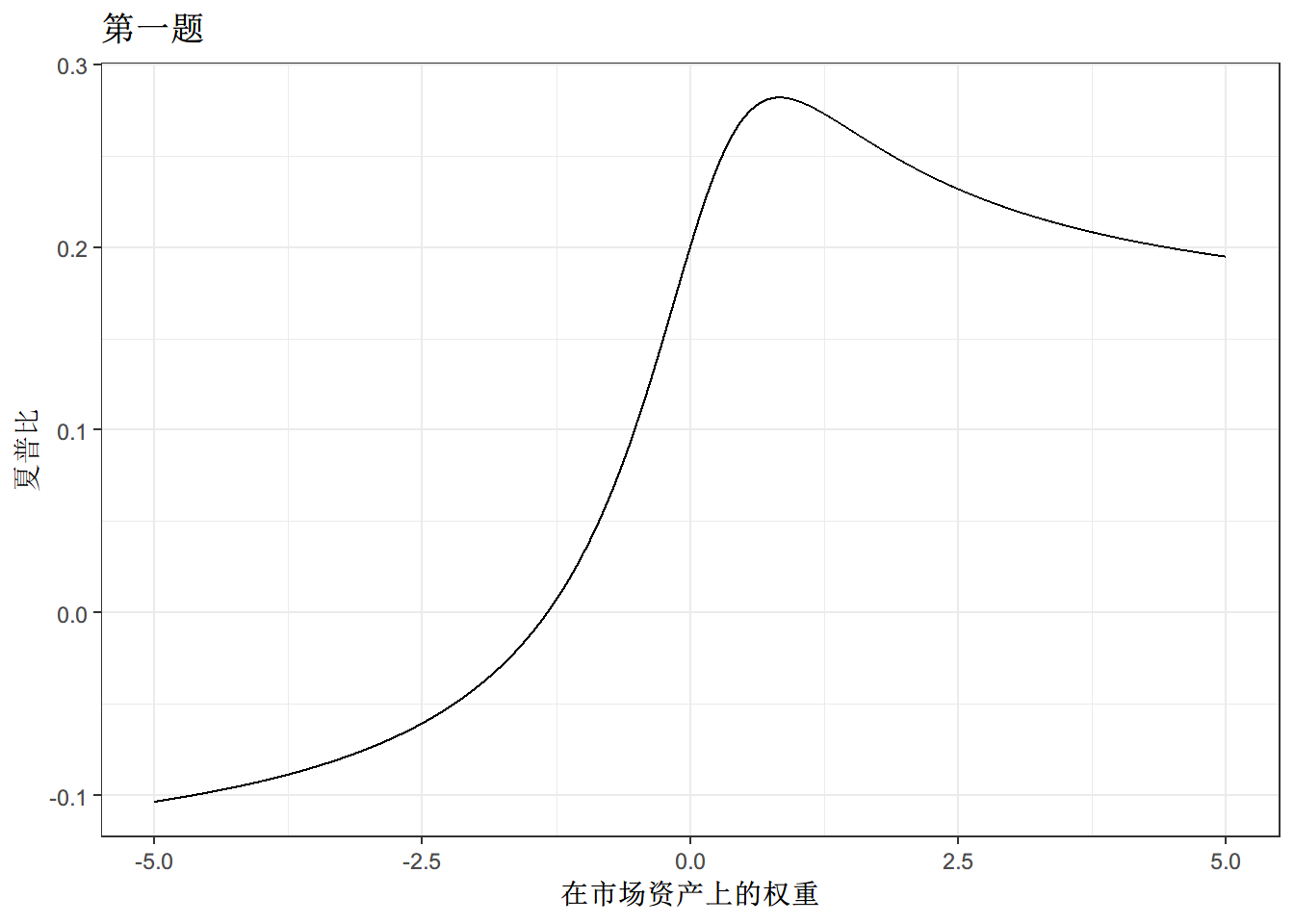
第一题

sr <- c()  # 先生成两个空容器，存储目标函数夏普比和对应的权重
w <- c()
# 写下目标函数
srr <- function(w){
  res = (0.4/100+(0.3/100)*w)/
    sqrt(w^2*(2.5/100)^2+(1-w)^2*(2/100)^2+(0.0625/100)*(w-w^2))
}

#循环，存储对应值，画图
for (i in seq(-5,5,by = 0.0005)){ 
  res = srr(i)
  sr <- append(sr,res)
  w <- append(w,i)
}
max(sr)

## [1] 0.2818255

pacman::p_load(tidyverse)

df <- tibble(x=w,y=sr)

ggplot(df,aes(x,y)) + geom_line()+ theme_bw()+
  xlab("在市场资产上的权重")+ylab("夏普比")+
  ggtitle("第一题")

optimize(srr,c(-100,100),maximum = T) #直接用包寻找最大化值，放入函数和取值范围

## $maximum
## [1] 0.8322294
## 
## $objective
## [1] 0.2818256

第二题

市场上的无风险利率为2％，市场组合（相对无风险利率）的超额回报率是6％，市场组合的波动率（标准差）为15％。市场中有一家名为XYZ的公司，其红利支付的波动率为20％，红利支付与市场组合之间的相关系数为0.9

（a）若XYZ公司股票明年每股预期红利支付为1元，且未来红利支付的预期增长率为5％，请计算这只股票现在的价格应该是多少?

（b）若XYZ公司股票明年每股预期红利支付仍然是1元，明年到后年的红利预期增长率为10％，后年之后的红利预期增长率都为5％。请计算在这样的红利支付预期下，这只股票现在的价格应该是多少。

第三题，请同学们自行练习，qq群作业提交，4月30日提交

经济中存在两种风险资产:股票A与股票B。在某段时间内，股票A的年平均回报率为8％，股票B的年平均回报率为12％。股票A和股票B的年回报率标准差分别为15％与20％。两只股票回报率之间的相关系数为0.5。经济中还存在一种无风险资产，每年可以产生4％的无风险利率。请问:

（a）用这三种资产构造出来的资产组合中，能够获得的最高夏普比是多少？

（b）在这样的资产市场中，市场组合的构成比例是怎样的？

（c）在这样的市场状况下，资本市场线（CML）与证券市场线（SML）的公式形式是怎样的？

（d）假设新出现了一位杰出的投资经理，他的资产组合相对问题（b）中求取的市场组合的B＝0.5，其资产组合与市场组合的相关系数为0.5，而该资产组合的Alpha为3％。请问，如果把这位投资经理的资产组合也利用上，投资者能获得的最高夏普比是多少？