CAPM模型的简单实现

A股数据资本资产定价模型的演示

A股数据资本资产定价模型的演示

基本模型回顾

FAMA在2004年写了一个比较好的文献

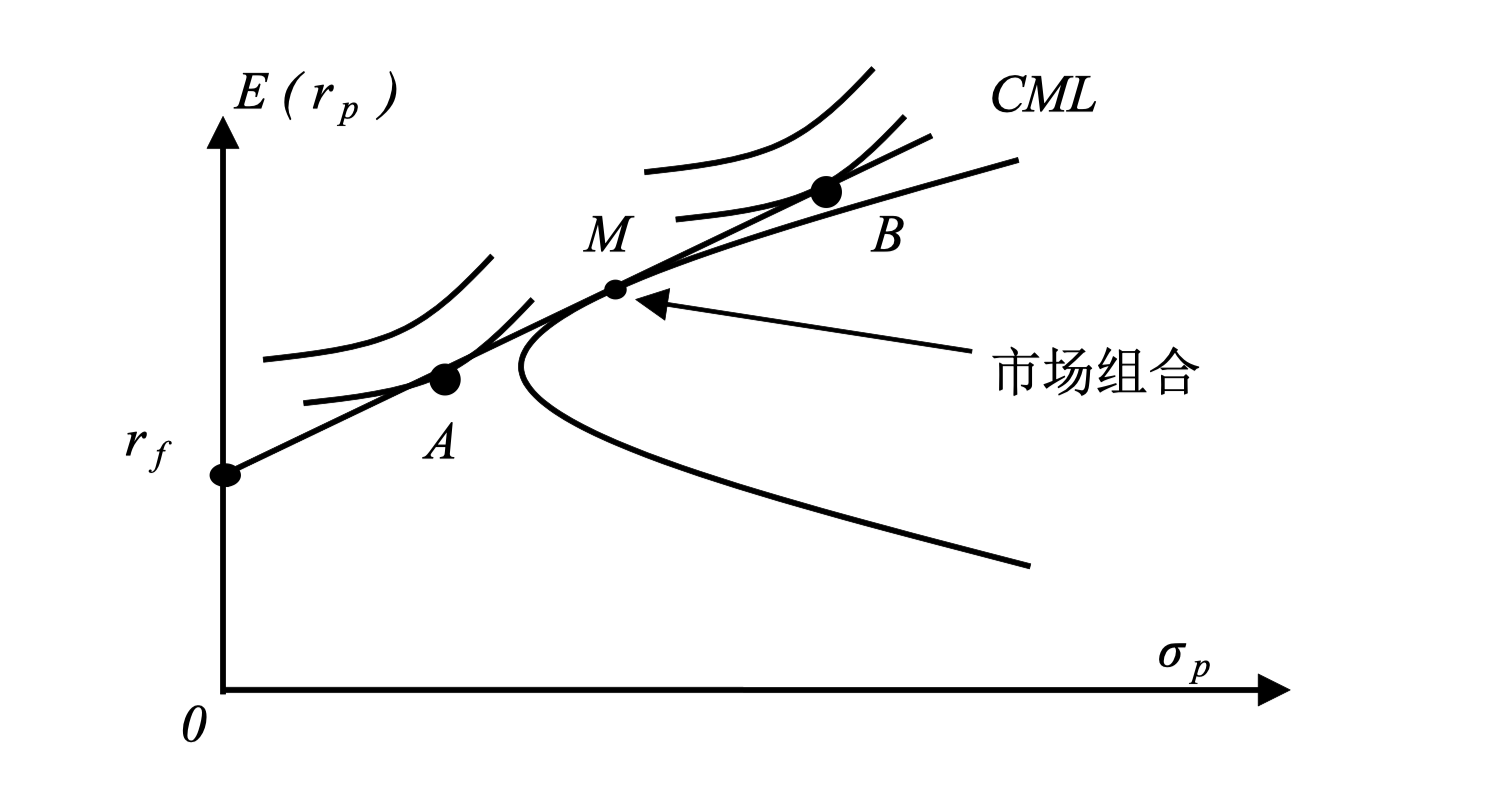
前面课程对均值方差模型进行了介绍，马科维茨(Markowitz)提出了投资组合选择理论，认为最佳投资组合应当是，风险厌恶的投资者的无差异曲线和资产组合的有效边界线的交点。

如果存在市场组合和无风险组合，且投资不存在买空限制的情况下，不同风险偏好的投资者会再无风险资产与市场资产组合的有效边界的切点组成的射线上进行资产分配。如下所示：

投资者在选择资产时会在收益和风险之间做出平衡：当风险一样时，会选择预期收益最高的资产；而预期收益一样时，会选择风险最低的资产。

CAPM模型

1964年，威廉-夏普(William Sharp)等则在马科维茨基础上提出的单指数模型，将市场组合引入均值-方差模型，极大地简化了计算，他们认为获得了市场任意资组合的收益与某个共同因素之间是有线性关系，最终将其发展为资本资产定价模型(Capital Asset Pricing Model, CAPM)。

具体来说，在CAPM公式下，如果所有投资者都采用均值方-差分析来确定其最优组合，那么在理想的状况下，均衡时的不同资产的预期回报率之间会具有一种线性关系—— $β$ 越高的资产期望回报率越高； $β$ 越低的资产期望回报率越低。

$E (r_{i}) - r_{f} = β_{i} [E (r_{M}) - r_{f}]$

其中：

$E (r_{i})$ 是资产或资产组合i的期望收益率
$r_{f}$ 是无风险资产的回报率
$E (r_{M})$ 是市场组合的期望回报率

资产组合构成及使用的包

- 中证500(000905.SH)

- 中国平安(601318.SH)

- 国海证券(000750.SZ)

- 东方园林(002310.SZ)

- 申达股份(600626.SH)

各个资产所占比例为20%，使用沪深300(000300.SH)作为市场组合，假设无风险利率为年化2%

我们使用tidyverse,tidyquant,Tushare,timetk进行数据获取、清理、分析及可视化。

数据获取及清洗

pacman::p_load(tidyquant,tidyverse,timetk,Tushare,DT)

api <- pro_api(token = '5adce34e8c81bf7085828754a8e09590c3630032d0f61aad6483eaaa')
bar <- pro_bar(token = '5adce34e8c81bf7085828754a8e09590c3630032d0f61aad6483eaaa')

zz500 <- api(api_name = 'index_daily',ts_code='000905.SH',start_date="20140101",
             end_date='20200407') 
pingan <- bar(ts_code='601318.SH',start_date="20140101",
              end_date='20200407',adj="qfq")
ghzq <- bar(ts_code='000750.SZ',start_date="20140101",
              end_date='20200407',adj="qfq")
dfyl <- bar(ts_code='002310.SZ',start_date="20140101",
              end_date='20200407',adj="qfq")
sdgf <- bar(ts_code='600626.SH',start_date="20140101",
              end_date='20200407',adj="qfq")
base <- api(api_name = 'index_daily',ts_code = '000300.SH',
             start_date='20140101', end_date = '20200407')
hs300 <- api(api_name = 'index_daily',ts_code = '000300.SH',
             start_date='20140101', end_date = '20200407')

数据读取后，观察一下数据行数，发现东方园林只有1316行，2014年1月1日到2020年4月7日所有交易日中证500指数有1526条记录，因此我们可以怀疑部分股票存在停牌问题。

为了处理缺失数据的一个思路是将缺失的日期全部删除，只分析5个资产都具有数据的日期

本文使用周频率进行演示。使用tidyquant中的tq_transmute进行收益率计算

week_ret <- function(x) {
  name = x$ts_code[1]
  df = x %>%  dplyr::mutate(trade_date = as.Date(trade_date,format="%Y%m%d"))
  res = df %>% tq_transmute(select = close,
                 mutate_fun = periodReturn,
                 period = 'weekly',
               col_rename = name)
  return(res)
}

zz500_r <- week_ret(zz500)
pingan_r <- week_ret(pingan)
ghzq_r <- week_ret(ghzq)
dfyl_r <- week_ret(dfyl)
sdgf_r <- week_ret(sdgf)
base_r <- week_ret(base)
hs300_r <- week_ret(hs300)

## 我们使用了一个自建函数，当然大家可以将之前的单个资产放到一个列表里，然后用 apply函数一次性处理这些转换过程

# 数据还是有比较大的缺失，因此我们使用左合来处理缺失数据

# 用交易日期作为key进行合并
df <- dfyl_r %>% left_join(pingan_r,by='trade_date' ) %>% left_join(ghzq_r,by='trade_date') %>% 
  left_join(sdgf_r,by='trade_date') %>% left_join(zz500_r) %>%
  left_join(hs300_r,by='trade_date')

## Joining, by = "trade_date"

f <- function(x){
  res = x - ((1+0.02)^(1/52)-1)
  return(res)
}

df2<- df[,-1] %>% mutate_all(f) %>% na.omit()

beta <- list()
for (i in colnames(df2)) {
  beta[[i]] = lm(df2[[i]]~`000300.SH`,data=df2)
}
## 这里我们使用回归的方式获得几个资产的beta
for (i in beta){
  print(i$coefficients[2])
}

## `000300.SH` 
##    1.057965 
## `000300.SH` 
##    1.167931 
## `000300.SH` 
##    1.277917 
## `000300.SH` 
##   0.9243951 
## `000300.SH` 
##    0.923485 
## `000300.SH` 
##           1

df_t <- na.omit(df) %>% tk_xts(silent = T)
# 将df转换为时间序列数据

手动计算各资产和组合的beta

我们知道： ${\hat{β}}_{i} = \frac{cov ({\tilde{r}}_{i}, {\tilde{r}}_{M})}{var ({\tilde{r}}_{M})} = \frac{σ_{i M}}{σ_{M}^{2}}$

在计算中务必注意无风险利率中，年收益率转换到周收益率

week_f_return <- (1+0.02)^(1/52)-1
df_t <- df_t - week_f_return #对于每个资产的回报率都减去无风险利率得到风险升水
dfyl_beta <- cov(df_t$`002310.SZ`,df_t$`000300.SH`)/var(df_t$`000300.SH`)
pingan_beta <- cov(df_t$`601318.SH`,df_t$`000300.SH`)/var(df_t$`000300.SH`)
ghzq_beta <- cov(df_t$`000750.SZ`,df_t$`000300.SH`)/var(df_t$`000300.SH`)
sdgf_beta <- cov(df_t$`600626.SH`,df_t$`000300.SH`)/var(df_t$`000300.SH`)
zz500_beta <-cov(df_t$`000905.SH`,df_t$`000300.SH`)/var(df_t$`000300.SH`)

组合的beta等于各资产的beta与其权重的线性组合，那么我们可以轻松的到组合的beta

port_beta <- t(matrix(rep(0.2,5),nrow=5)) %*% matrix(c(dfyl_beta,pingan_beta,ghzq_beta,sdgf_beta,zz500_beta),nrow = 5)
print(paste("我们构建的投资组合的beta为：",port_beta))

## [1] "我们构建的投资组合的beta为： 1.07033846432365"

df_long <- df %>% select(-`000300.SH`) %>%
  pivot_longer(-trade_date,names_to = "names",values_to = "returns")

m_return <- df %>% select(trade_date,`000300.SH`)
df_long_beta <- df_long %>% left_join(m_return,by="trade_date") %>%
  rename(Rb = `000300.SH`) %>% mutate(returns = returns-week_f_return)

beta_builtin_tq <- 
  df_long_beta %>% 
  group_by(names) %>%
  tq_performance(Ra = returns, 
                 Rb = Rb, 
                 performance_fun = CAPM.beta
                ) 
beta_builtin_tq

## # A tibble: 5 x 2
## # Groups:   names [5]
##   names     CAPM.beta.1
##   <chr>           <dbl>
## 1 002310.SZ       1.06 
## 2 601318.SH       1.16 
## 3 000750.SZ       1.28 
## 4 600626.SH       0.933
## 5 000905.SH       0.922

port <- t(matrix(rep(0.2,5),nrow=5)) %*%
  as.matrix(beta_builtin_tq$CAPM.beta.1,nrow=5)
port

##          [,1]
## [1,] 1.071526

手动计算出的组合beta为1.0703，tidyquant包计算出来的beta是1.071。基本差距不大

张剑

2020/04/18