投资组合优化——以A股五个资产为例

在均值方差分析框架下，投资组合优化的目标可以由一下两个等同(对偶)的目标进行描述

1. 给定一定的收益率，投资组合的方差（风险最小）

2. 给定一定的风险，投资组合的收益大

如果是三个资产，假设三个资产均不相关，上述过程可以用数学表示为：

\[\begin{aligned} &\min _{w_{1}, w_{2}, m_{3}} w_{1}^{2} \sigma_{1}^{2}+w_{2}^{2} \sigma_{2}^{2}+w_{3}^{2} \sigma_{3}^{2}\\ &\text { s.t. } \quad w_{1} \bar{r}_{1}+w_{2} \bar{r}_{2}+w_{3} \bar{r}_{3}=\bar{r}\\ &w_{1}+w_{2}+w_{3}=1 \end{aligned}\]

给出拉格朗日函数及其一阶条件：

\[L=w_{1}^{2} \sigma_{1}^{2}+w_{2}^{2} \sigma_{2}^{2}+w_{3}^{2} \sigma_{3}^{2}+\lambda\left[w_{1} \bar{r}_{1}+w_{2} \bar{r}_{2}+w_{3} \bar{r}_{3}-\bar{r}\right]+\mu\left[w_{1}+w_{2}+w_{3}-1\right]\]

\[\frac{\partial \mathcal{L}}{\partial w_{i}}=0 \Rightarrow 2 \sigma_{i}^{2} w_{i}+\lambda \bar{r}_{i}+\mu=0\]

我们可以对任意的 \(\bar r\) 计算出最优的组合权重，有了对应权重，我们可以计算出对应不同的\(\bar r\)最优的权重，以及最优权重对应的投资组合的收益和标准差。

将这些最优的投资组合的收益——标准差(有了收益和标准差就有了一个点),将这些点连接成线，就可以得到投资组合的有效边界。

这个问题由变成了一个数学优化问题，我们继续以A股5中资产，2014年1月1日至2020年4月7日的月度收益率为基准，演示一系列投资组合优化问题。

上述代码，进行了数据读入，数据合并与数据转换，我们看一下最终转换的数据的样子

stock_long_m_r %>% datatable() %>% 
  formatRound(columns = "Ra" ,digits = 3) # 后面的format选项是控制Ra也就是我们的月度收益率的小数点位数

接下来计算最优投资组合下的权重问题,我们直接使用tseries包中的portfolio.optim函数进优化，如果希望自己进行优化的，也可以使用quadprog 二次优化包自行计算

portfolio.optim 有几个重要参数，先做一个简单介绍：

1. x ：由一系列收益组成的数值矩阵或多元时间序列
   
2. pm ： 期望的平均投资组合收益 ，默认给的值是mean(x)
3. riskless 有无风险借贷率的逻辑说明 T or F

# 先将数据处理成时间序列

wide_return_m <- stock_long_m_r %>%
  pivot_wider(names_from = ts_code,values_from = Ra) # 将数据处理成宽形

wide_return_m <- wide_return_m %>%
  tk_xts(silent = T) #将数据处理成时间序列

res<-tseries::portfolio.optim(wide_return_m) #调用tseries中的portfolio.optim包

weight_m<-res$pw
name <- c('中国平安','中国人寿','中国太保','工商银行','中证500')
wei <- tibble(weight = weight_m , name = name)
g5 <-ggplot(wei ,aes(x=name,y=weight,fill=name)) + geom_col() +
  theme_tq() + tidyquant::scale_fill_tq() +
  scale_y_continuous(labels = scales::percent)

print(res$pm/res$ps) ## 回报该权重下的夏普比例

## [1] 0.212

ggplotly(g5)

我们的到了投资组合的最优权重w，以及在该权重下的收益率与标准差。我们可以通过调整pm参数，来调整期望的平均投资组合收益

同时不同期望收益率pm下面的投资组合的值，获得一系列最优投资的均值和标准差。

将这些均值和标准差在坐标系下的点连接起来就得到了有效投资边际

bar_r <- seq(0.8,1.5,by =0.05)
ret <- c()
sd <- c()

for (i in seq(0.8,1.5,by =0.05)){
  port = tseries::portfolio.optim(wide_return_m , pm = i * mean(wide_return_m))
  ret = append(ret,port$pm)
  sd = append(sd,port$ps)
}

# 允许卖空
ret_2 <- c()
sd_2 <- c()
for (i in seq(0.8,1.5,by =0.05)){
  port = tseries::portfolio.optim(wide_return_m , pm = i * mean(wide_return_m),shorts=T)
  ret_2 = append(ret_2,port$pm)
  sd_2 = append(sd_2,port$ps)
}


eef <- tibble(bar_r = bar_r ,return_short =ret,
              sd_short =sd,return=ret_2,sd=sd_2) %>%
  select(- return_short)

eef <- eef %>%
  pivot_longer(cols = - c(bar_r,return),names_to = "names", values_to = 'value')


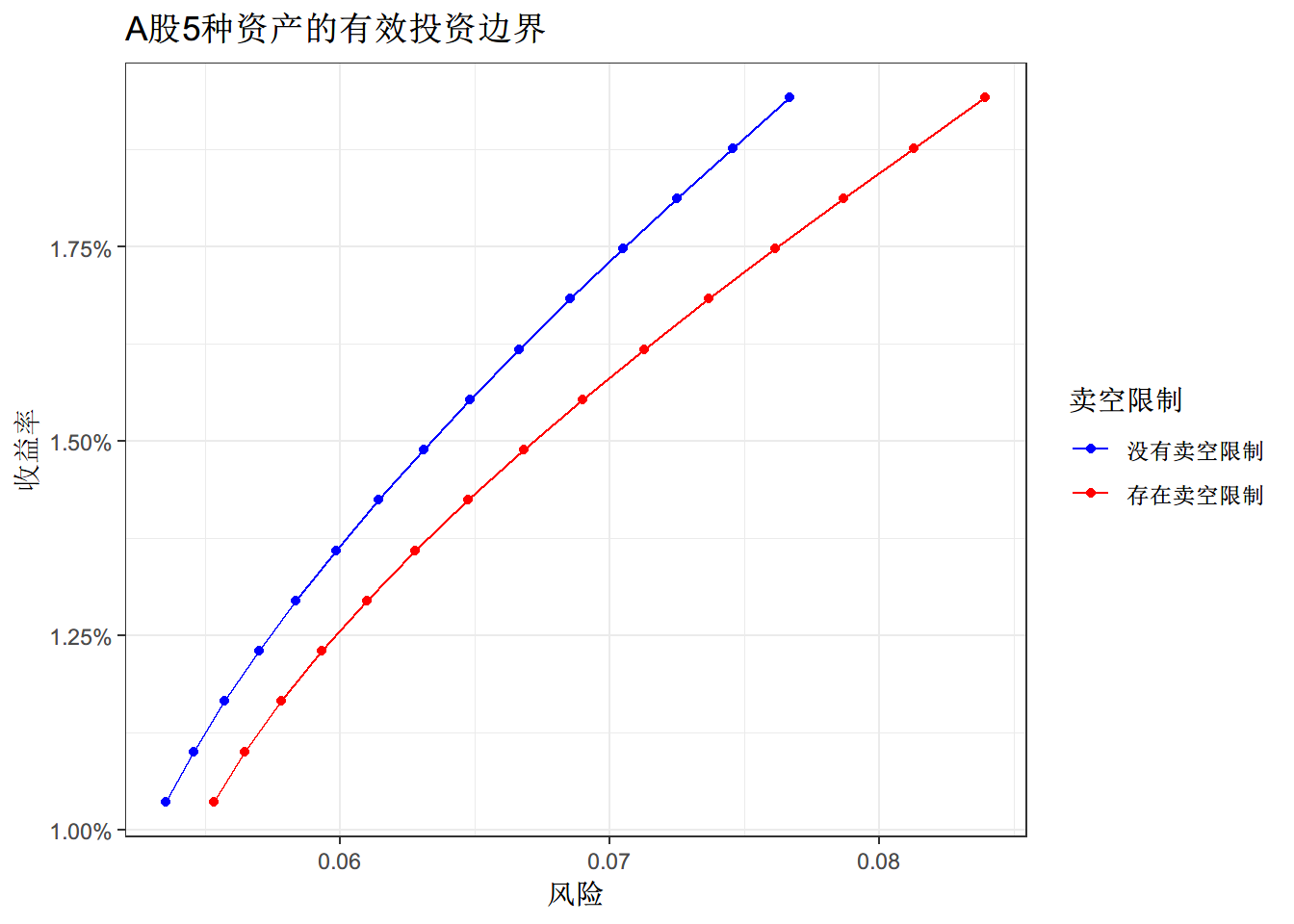
ggplot(eef,aes(x=value,y=return,color=names)) + geom_line() +geom_point() + 
  theme_bw() + xlab("风险") + ylab("收益率") +
  scale_y_continuous(labels = scales::percent)+
  ggtitle('A股5种资产的有效投资边界')+labs(color='卖空限制')+
  scale_color_manual(labels = c("没有卖空限制", "存在卖空限制"), values = c("blue", "red"))

核心思路：

1. 随机生成一系列权重；
2. 将权重带入投资组合，进而计算组合的收益和标准差，以及夏普比；
3. 找出最小风险的投资组合，找出最大夏普比的投资组合。

num_port <- 1500
all_wts <- matrix(nrow = num_port,
                 ncol = 5) # 这里用5，

port_returns <- vector('numeric', length = num_port)
port_risk <- vector('numeric', length = num_port)
sharpe_ratio <- vector('numeric', length = num_port)

for (i in seq_along(port_returns)){
  wts <- runif(5) ## 构成组合的资产数量
  wts <- wts/sum(wts)
  all_wts[i,] <- wts

  port_return <- stock_long_m_r %>%
    tq_portfolio(assets_col = ts_code,returns_col = Ra,
                 weights = wts,col_rename = "p")

  port_returns[i] <- mean(port_return$p)

  port_risk[i] <- sd(port_return$p)

  sharpe_ratio[i] <- mean(port_return$p)/sd(port_return$p)

}

portfolio_values <- tibble(Return = port_returns,
                           Risk = port_risk,
                           SharpeRatio = sharpe_ratio)
all_wts <- tk_tbl(all_wts)

colnames(all_wts) <- c('中国平安','中国人寿','中国太保','工商银行','中证500')
portfolio_values <- tk_tbl(cbind(all_wts, portfolio_values))
min_var <- portfolio_values[which.min(portfolio_values$Risk),]
max_sr <- portfolio_values[which.max(portfolio_values$SharpeRatio),]
min_var

## # A tibble: 1 x 8
##   中国平安 中国人寿 中国太保 工商银行 中证500  Return   Risk SharpeRatio
##      <dbl>    <dbl>    <dbl>    <dbl>   <dbl>   <dbl>  <dbl>       <dbl>
## 1   0.0258   0.0362    0.158    0.463   0.317 0.00937 0.0585       0.160

max_sr

## # A tibble: 1 x 8
##   中国平安 中国人寿 中国太保 工商银行 中证500 Return   Risk SharpeRatio
##      <dbl>    <dbl>    <dbl>    <dbl>   <dbl>  <dbl>  <dbl>       <dbl>
## 1    0.722   0.0575 0.000569   0.0502   0.170 0.0186 0.0830       0.224

min_var_long <- min_var %>%
  pivot_longer(cols = -c(Return,Risk,SharpeRatio) ,names_to = "names" , values_to = "weight") %>%
  mutate(names = as.factor(names))


g<-ggplot(min_var_long,aes(x = fct_reorder(names,weight), y = weight, fill = names)) +
  geom_bar(stat = 'identity') + theme_tq() + tidyquant::scale_fill_tq() + xlab('各类资产')+
  ylab('权重')+scale_y_continuous(labels = scales::percent) +
  ggtitle('模拟500次选出的投资组合方差最小的权重比例')

ggplotly(g)

max_sr_long <- max_sr %>%
  pivot_longer(cols = -c(Return,Risk,SharpeRatio) ,names_to = "names" , values_to = "weight") %>%
  mutate(names = as.factor(names))


g_2<-ggplot(max_sr_long,aes(x = fct_reorder(names,weight), y = weight, fill = names)) +
  geom_bar(stat = 'identity') + theme_tq() + tidyquant::scale_fill_tq() + xlab('各类资产')+
  ylab('权重')+scale_y_continuous(labels = scales::percent) +
  ggtitle('模拟500次选出的投资组合夏普比率最大的权重比例')

ggplotly(g_2)

g_3 <- portfolio_values %>%
  ggplot(aes(x = Risk, y = Return, color = SharpeRatio)) +
  geom_point() +
  theme_classic() +
  scale_y_continuous(labels = scales::percent) +
  scale_x_continuous(labels = scales::percent) +
  geom_point(aes(x = Risk,
                 y = Return), data = min_var, color = 'red') +
  geom_point(aes(x = Risk,
                 y = Return), data = max_sr, color = 'red') +
  labs(x = '月度风险',
       y = '月度收益率',
       title = "A股五资产的投资组合优化与有效边界")

ggplotly(g_3)

上面的两个红点分别对应了最低风险组合和最大夏普比例组合