目标
本次主要实现投资组合收益、累计收益、标准差、夏普比率的计算与实现。同时使用介绍再平衡策略在投资组合中的简单应用。
主要接口、包及流程：
- 使用Tushare下载原始资产数据；
- 利用tidyquant、tidyverse、timetk对原始资产数据进行加工，使其满足教材所需经典条件；
- 实现50-50的再平衡策略，测试月度再平衡和季度在平衡策略；
回归投资组合基本思路
投资组合收益率
1.日收盘价转换为日收益率
\[R_{t 2}=\frac{P_{t 2}-P_{t 1}}{P_{t 1}}\]
2.日收益率转换为年度收益率，假设一天有252个交易日。周收益率和日收益率同理可得
\[\text {平均年化收收益率}= (1 + R_t)^{252}-1\]
3. 投资组合的收益率与方差(两资产)
\[E\left(r_{P}\right)=w_{A} \cdot E\left(r_{A}\right)+w_{B} \cdot E\left(r_{B}\right)\] \[w_A+w_B=1\] \(w_A\)和\(w_B\)分别是事前投资与A资产与B资产的权重，\(E(r_A)\)和\(E(r_B)\)分别是A与B标的资产的历史期望收益率。
两种资产组合的方差为： \[\begin{aligned} \sigma^{2}\left(r_{P}\right)=& w_{A}^{2} \sigma^{2}\left(r_{A}\right)+w_{B}^{2} \sigma^{2}\left(r_{B}\right)+2 w_{A} w_{B} \operatorname{Cov}\left(r_{A}, r_{B}\right) \end{aligned}\]
\[\rho_{AB}=\frac{COV(A,B)}{\sigma_{A} \sigma_{B}}\]
\[COV(A,B)=\rho_{AB} \cdot \sigma_{A} \sigma_{B}\]
其中\(\rho_{AB}\)为资产A与资产B的相关系数
如果多个资产，用简洁的矩阵形式表示为：
\[\begin{array}{c} \delta^{2}\left(r_{p}\right)=\sum \sum_{i=2}^{n} w_{i} w_{j} \operatorname{cov}\left(r_{i}, r_{j}\right) \\ E\left(r_{p}\right)=\sum w_{i} r_{i} \end{array}\]
下载原始数据
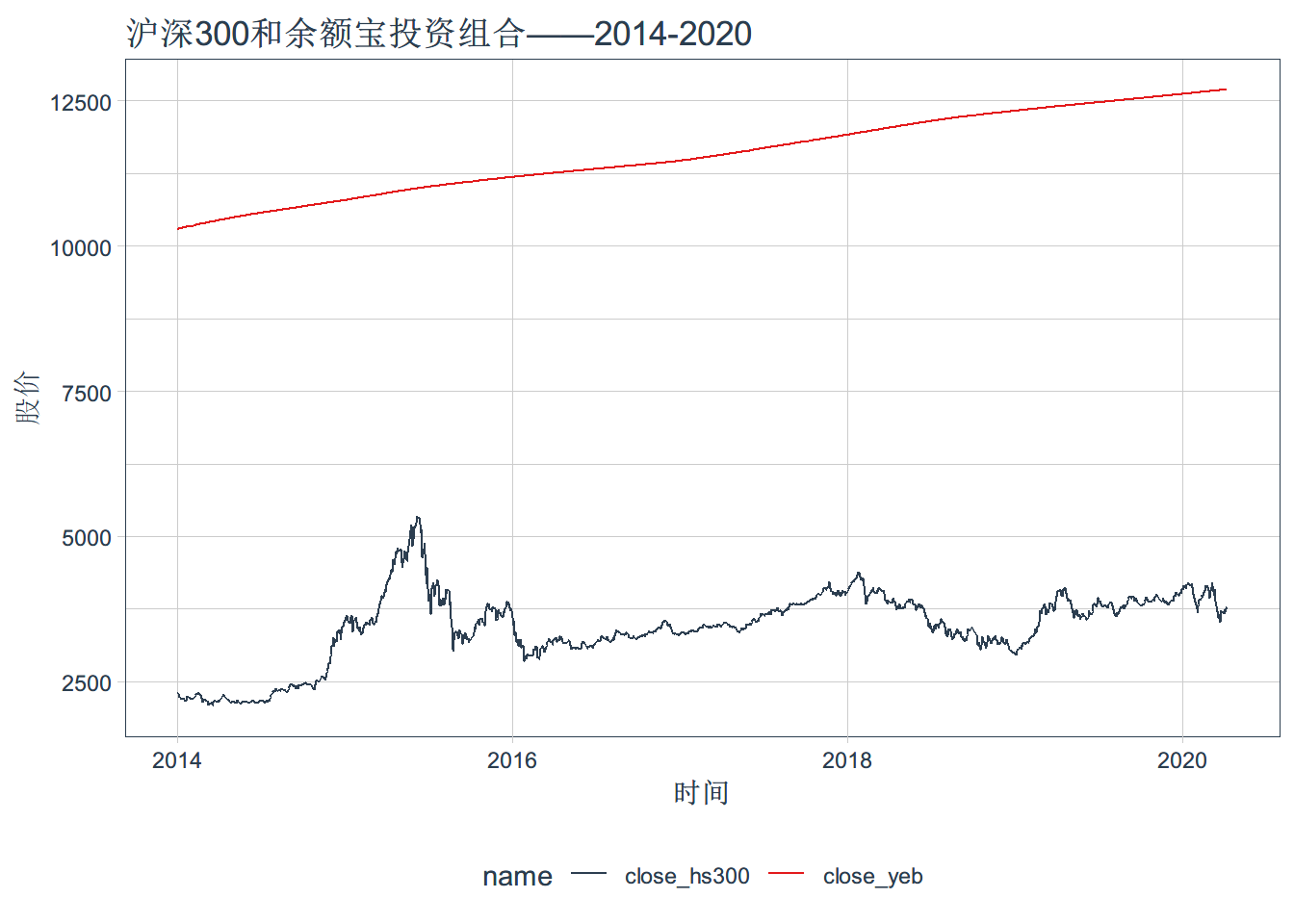
我们构建一个50-50的两资产的投资组合，即\(w_A = 50%\),\(w_B =50%\) 资产标的我们选择沪深300指数(000300.SH)以及余额宝对应的天弘基金(000198.OF)。
pacman::p_load(tidyquant,tidyverse,timetk,Tushare,DT)
api <- pro_api(token = '5adce34e8c81bf7085828754a8e09590c3630032d0f61aad6483eaaa')
bar <- pro_bar(token = '5adce34e8c81bf7085828754a8e09590c3630032d0f61aad6483eaaa')
hs300 <- api(api_name = 'index_daily',ts_code = '000300.SH',
start_date='20140101', end_date = '20200407')
hs300 <- hs300 %>%
select(ts_code,trade_date,close) %>%
mutate(trade_date = as.Date(trade_date,format="%Y%m%d") )
yeb <- api(api_name = 'fund_nav',ts_code = '000198.OF',market ='O')
# 基金净值接口，无法设定开始时间，数据下载后需要自行处理
yeb <- yeb %>%
rename(close = adj_nav ) %>%
mutate(trade_date = as.Date(end_date,format="%Y%m%d")) %>%
filter(trade_date >= as.Date('20140101',format="%Y%m%d"),trade_date <= as.Date('20200407',format="%Y%m%d")) %>%
select(ts_code,trade_date,close)
# 合并数据，左合并，数据整理成long形
stock <- hs300 %>%
left_join(yeb,by="trade_date", suffix=c('_hs300','_yeb')) %>%
as_tibble()
stock_long <- stock %>%
pivot_longer(cols = c(close_hs300,close_yeb),names_to = 'name',
values_to = 'price') %>%
select(name,trade_date,price) %>% drop_na()
stock_long %>% datatable()上面进行数据合并的时候，用了和之前不一样的方法，使用了left_jion这个函数，这个函数具体帮助见链接!!!。
左合并的主要思想是：保持“左”边的数据集为主集，“右”边的数据集配合“左”边数据集进行合并，合并的key是用by参数控制的，这里的key是匹配的关键词，也就是两个数据集里都具有的特征变量。在左合并时，如果右数据集大于左数据集，那么删除部分右边数据从而实现匹配左边数据的方式。
先看一下我们希望构建的两个资产的价格趋势
ggplot(stock_long,aes(x=trade_date,y = price,color=name))+
geom_line() + theme_tq() + xlab("时间") + ylab("股价") +
scale_color_tq() + ggtitle("沪深300和余额宝投资组合——2014-2020")
计算投资组合的收益率、组合的方差
使用tidyquant中的tq_portfolio来计算收益率，手动计算也完全没有问题，思路是把50-50权重合并到数据集上，生成一个新的组合收益率即可。
# 给出权重50-50
wts <- c(0.5,0.5)
#计算日收益率
stock_long_daily_r <-stock_long %>%
group_by(name) %>%
tq_transmute(select = price,
mutate_fun = periodReturn,
period = 'daily',
col_rename = "Ra")
stock_long_daily_r## # A tibble: 3,052 x 3
## # Groups: name [2]
## name trade_date Ra
## <chr> <date> <dbl>
## 1 close_hs300 2014-01-02 0
## 2 close_hs300 2014-01-03 -0.0134
## 3 close_hs300 2014-01-06 -0.0228
## 4 close_hs300 2014-01-07 -0.000284
## 5 close_hs300 2014-01-08 0.00175
## 6 close_hs300 2014-01-09 -0.00878
## 7 close_hs300 2014-01-10 -0.00782
## 8 close_hs300 2014-01-13 -0.00507
## 9 close_hs300 2014-01-14 0.00874
## 10 close_hs300 2014-01-15 -0.00176
## # ... with 3,042 more rowsport_daily_r <- stock_long_daily_r %>%
tq_portfolio(assets_col = name,
returns_col = Ra,
weights = wts,
col_rename = "port_RA")
port_daily_r## # A tibble: 1,526 x 2
## trade_date port_RA
## <date> <dbl>
## 1 2014-01-02 0
## 2 2014-01-03 -0.00663
## 3 2014-01-06 -0.0110
## 4 2014-01-07 -0.0000473
## 5 2014-01-08 0.000950
## 6 2014-01-09 -0.00422
## 7 2014-01-10 -0.00373
## 8 2014-01-13 -0.00220
## 9 2014-01-14 0.00433
## 10 2014-01-15 -0.000772
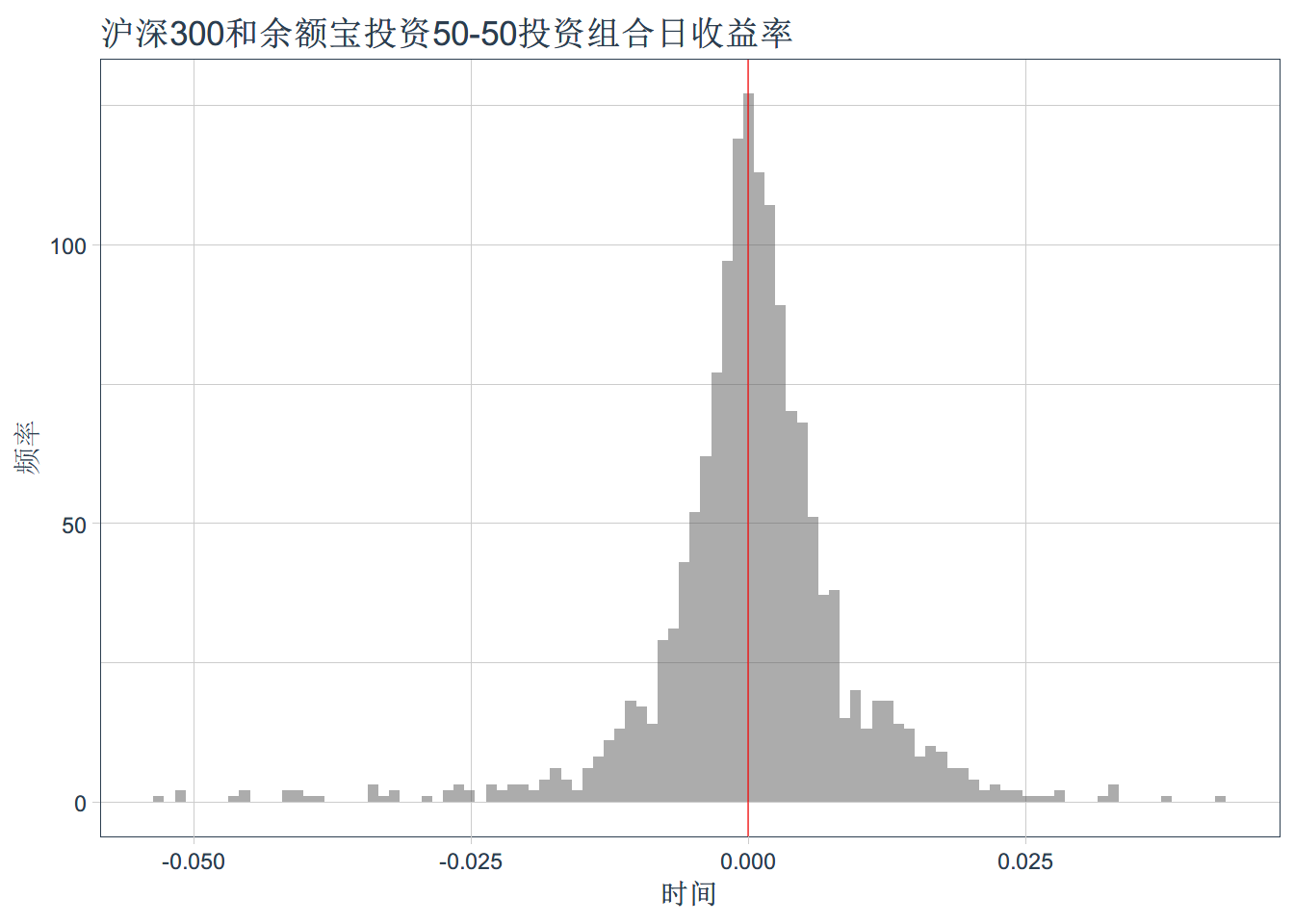
## # ... with 1,516 more rows展示我们构建的投资组合的收益率的分布情况
ggplot(port_daily_r , aes(x=port_RA)) +
geom_histogram(bins=100 ,alpha=0.5) + geom_vline(xintercept = 0,color='red',alpha=0.6)+
theme_tq() + xlab("时间") + ylab('频率')+
ggtitle('沪深300和余额宝投资50-50投资组合日收益率')
获得我们构建的投资组合的日收益率均值和标准差
#汇报组合均值和方差
paste("我们构建的组合的日收益率均值为：",mean(port_daily_r$port_RA, na.rm = TRUE))## [1] "我们构建的组合的日收益率均值为： 0.000275597816601841"paste("我们构建的组合的日收益率标准差为：",sd(port_daily_r$port_RA, na.rm = TRUE))## [1] "我们构建的组合的日收益率标准差为： 0.00883183214352526"组合的累计收益率(Cumulative portfolio returns)
投资者一般对日、月收益率不敏感，但是对累计收益率相对容易理解。上次的课程已经介绍过累计收益率的计算，只不过是计算单个资产，现在我们进行计算投资组合的累计收益率。
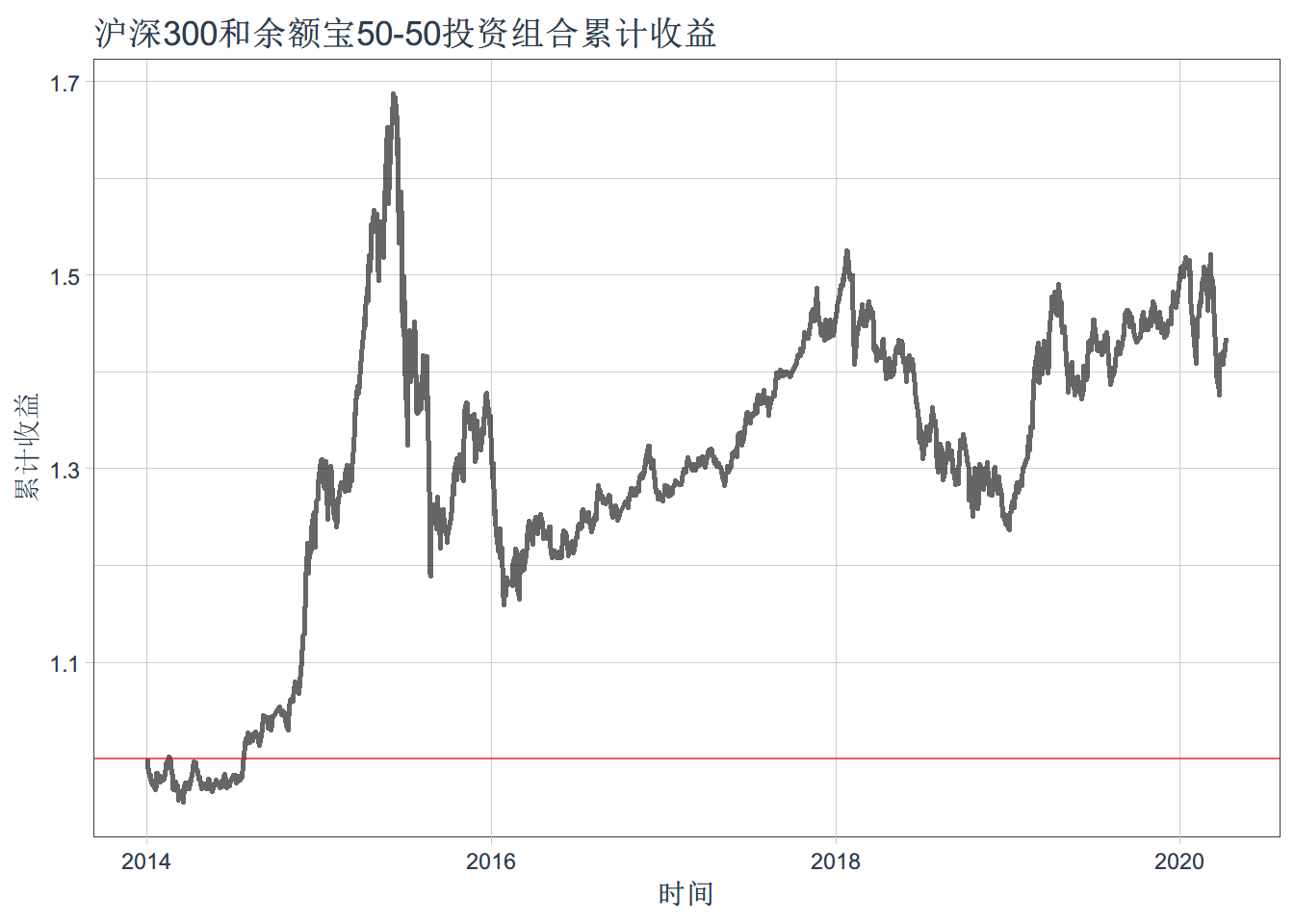
所谓累计收益率，在本例中可以理解为2014年1月1日投入1元钱，到2020年4月7日这一块钱变成了多少
port_cumulative_ret <- port_daily_r %>%
mutate(cr = cumprod(1 + port_RA))
#作图展示
ggplot(port_cumulative_ret,aes(x=trade_date,y=cr)) + geom_line(size=1.05,alpha=0.6)+
theme_tq() + xlab("时间") + ylab("累计收益")+
ggtitle("沪深300和余额宝50-50投资组合累计收益")+
geom_hline(yintercept = 1,color="red",alpha = 0.6)
50-50投资组合下的再平衡展示
思路
- 展示沪深300累计收益；
- 展示余额宝累计收益
- 展示不进行再平衡投资组合的累计收益
- 展示进行月度再平衡策略的投资组合累计收益
再平衡的核心逻辑
所谓再平衡就是通过定期的买入卖出操作维持投资组合的目标配比，和定投一样是一种简单的公式化操作。
再平衡的核心逻辑可以用四个点来概括，即通过公式化的定期操作，降低投资组合的波动风险，提升同等风险水平下的收益率，实现被动的高抛低吸。
对于50-50 组合来说，再平衡的操作流程： 1. 到达预定的再平衡时间，重新计算组合总净值； 2. 计算指数基金和货币基金的当前实际占比； 3. 卖出占比超过 50% 的资产，买出占比低于 50% 的资产，使比例重新回到 50:50。
具体2014年1月1日至2020年4月7日回测结果如下：
hs300_cr <- stock_long_daily_r %>%
filter(name=="close_hs300") %>%
mutate(cr = cumprod(1 + Ra))
yeb_cr <- stock_long_daily_r %>%
filter(name=="close_yeb") %>%
mutate(cr = cumprod(1 + Ra))
port_daily_r_rebanmonth <- stock_long_daily_r %>%
tq_portfolio(assets_col = name,
returns_col = Ra,
weights = wts,
rebalance_on = 'quarters',
col_rename = "port_RA")
port_cumulative_ret_reban <- port_daily_r_rebanmonth %>%
mutate(cr = cumprod(1 + port_RA))
fig<-ggplot()+
geom_line(data=hs300_cr,mapping = aes(x=trade_date,y=cr,color="沪深300"))+
geom_line(data=yeb_cr,mapping = aes(x=trade_date,y=cr,color='余额宝') ) +
geom_line(data=port_cumulative_ret,mapping = aes(x=trade_date,y=cr,color='无再平衡组合'))+
geom_line(data=port_cumulative_ret_reban,mapping = aes(x=trade_date,y=cr,color='季度再平衡组合')) +
theme_tq() + scale_color_tq() + xlab("时间") +
ylab("累计收益")+ ggtitle("50-50再平衡策略累计收益")
pacman::p_load(plotly)
ggplotly(fig,width = 900,height = 500)