两个资产的联合线的拟合
参考我们ppt上案例,使用软件对两个不同的相关性程度进联合线模拟
使用tidyver包绘图,DT包展示数据
参考ppt给出我们想画的两个资产默认的均值、标准差,同时两资产默认相关系数为0
可以自行调整函数参数
函数编好,大家也可以自行测试
pacman::p_load(tidyverse,DT)
sqx <- function(w,r_a=0.1,r_b=0.04,sd_a=0.05,sd_b=0.1,rho=0){
risk = sqrt(w^2*sd_a^2+(1-w)^2*sd_b^2+2*w*(1-w)*rho*sd_a*sd_b)
mean = w*r_a+(1-w)*r_b
res = tibble(mean=mean,risk=risk)
return(res)}
sqx(1.5)## # A tibble: 1 x 2
## mean risk
## <dbl> <dbl>
## 1 0.13 0.0901res_1 <- NULL
for (i in seq(-0.5,1.5,by=0.1)){
res_1 = rbind(res_1,sqx(i))}
res_1 %>% datatable()ggplot(res_1,aes(x=mean,y=risk)) + geom_point() + tidyquant::theme_tq()+
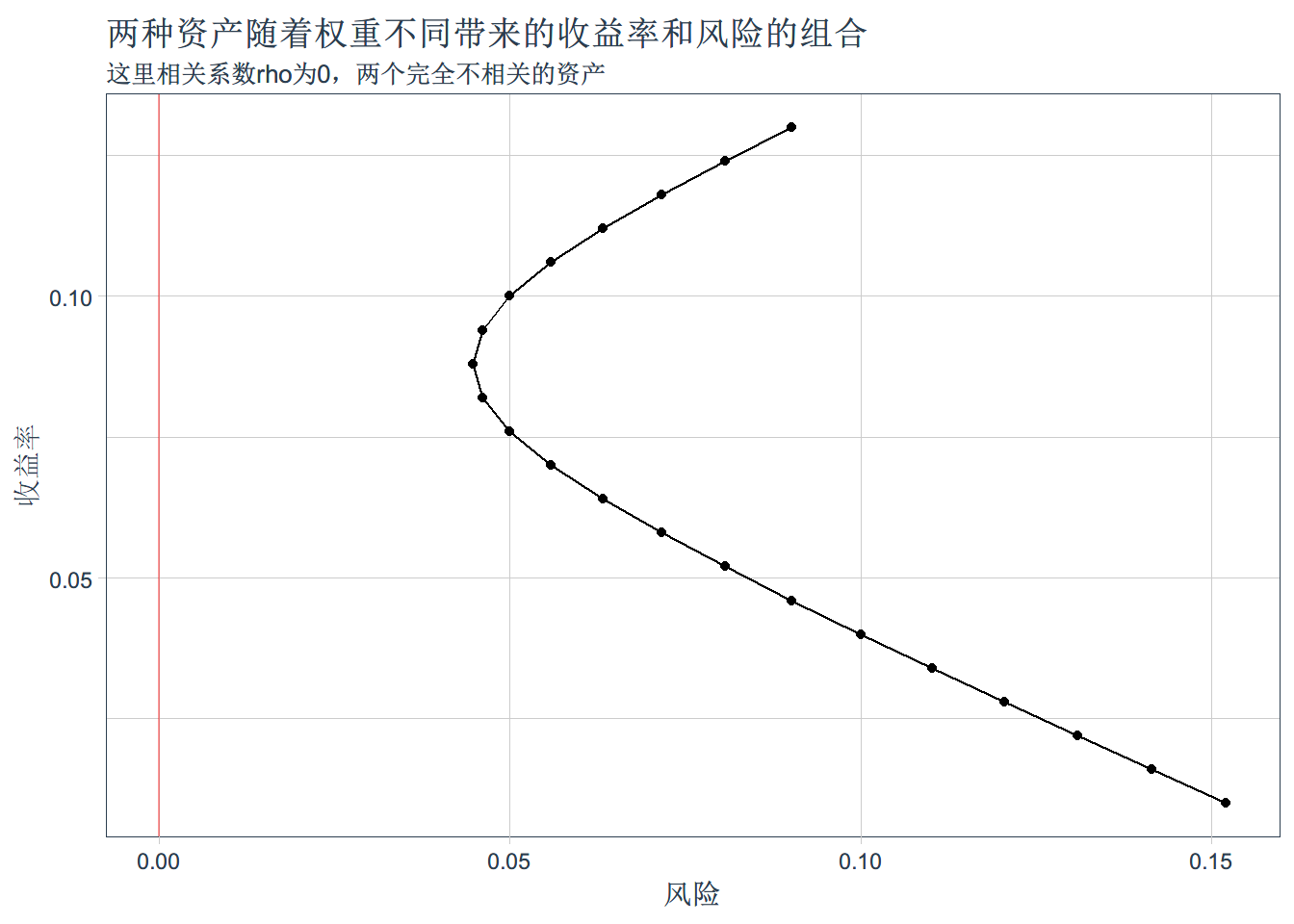
geom_line() + xlab('收益率') + ylab('风险') + ggtitle('两种资产随着权重不同带来的收益率和风险的组合',subtitle = '这里相关系数rho为0,两个完全不相关的资产') +coord_flip() +
geom_hline(yintercept = 0,color= 'red',alpha =0.4)res_2 <- NULL
for (i in seq(-0.5,3,by=0.1)){
res_2 = rbind(res_2,sqx(i, rho = -1))
}
res_2 %>% datatable()ggplot(res_2,aes(x=mean,y=risk)) + geom_point() + tidyquant::theme_tq()+
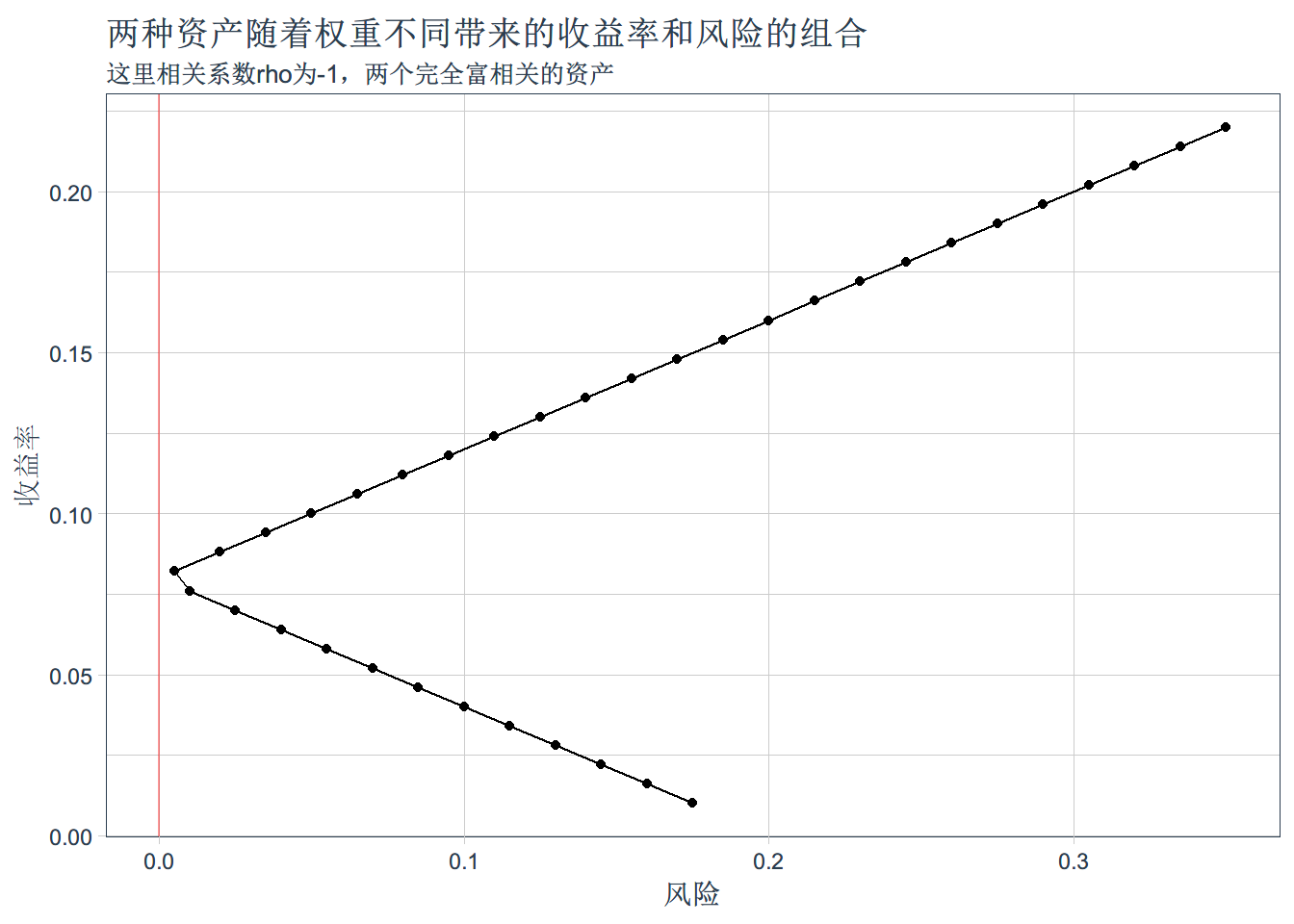
geom_line() + xlab('收益率') + ylab('风险') + ggtitle('两种资产随着权重不同带来的收益率和风险的组合',subtitle = '这里相关系数rho为-1,两个完全富相关的资产') +coord_flip()+
geom_hline(yintercept = 0,color= 'red',alpha =0.4)res_3 <- NULL
for (i in seq(-0.5,3,by=0.1)){
res_3 = rbind(res_3,sqx(i, rho = 1))
}
res_3 %>% datatable()ggplot(res_3,aes(x=mean,y=risk)) + geom_point() + tidyquant::theme_tq()+
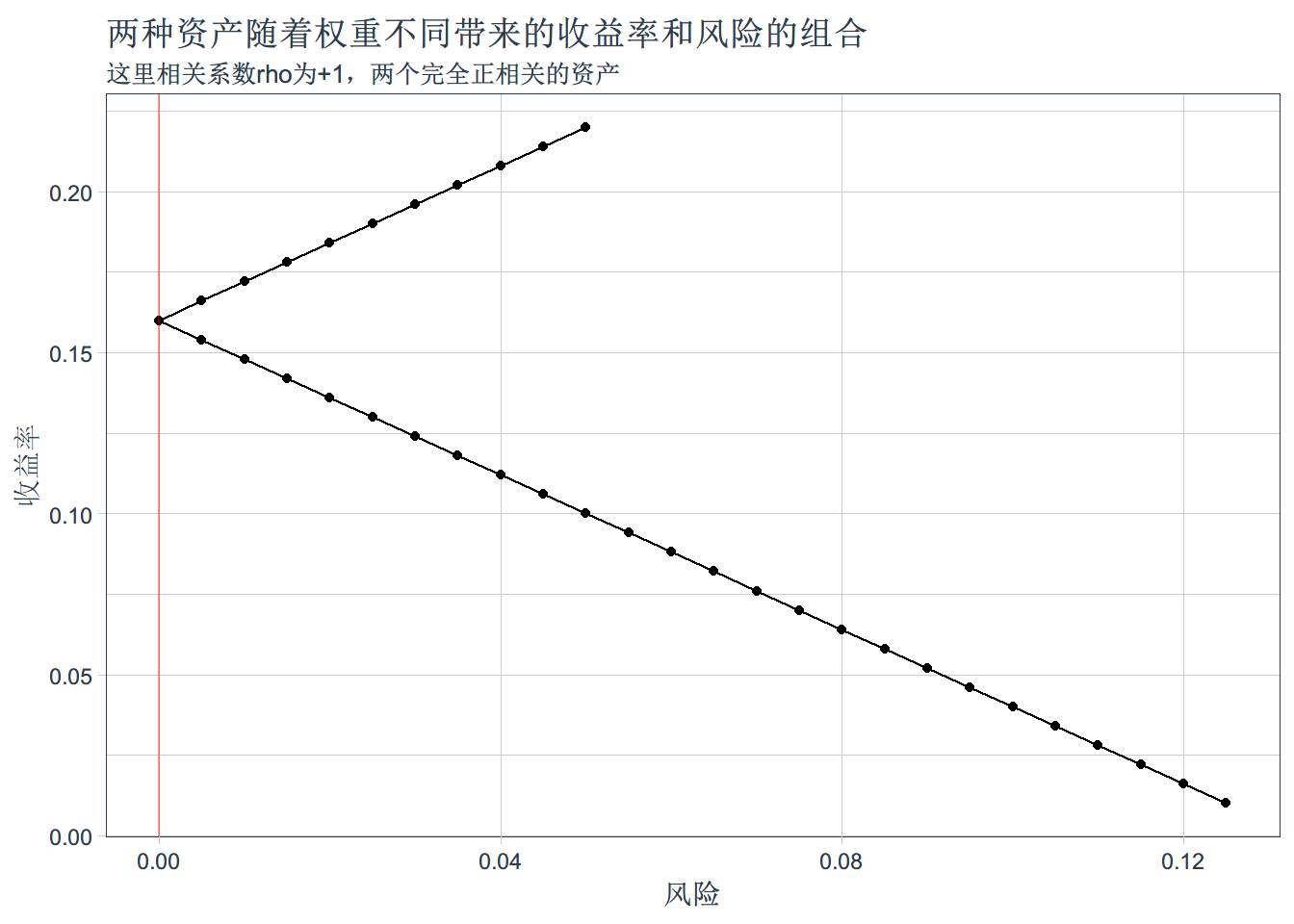
geom_line() + xlab('收益率') + ylab('风险') + ggtitle('两种资产随着权重不同带来的收益率和风险的组合',subtitle = '这里相关系数rho为+1,两个完全正相关的资产') +coord_flip()+
geom_hline(yintercept = 0,color= 'red',alpha =0.4)三个资产有效投资域的拟合
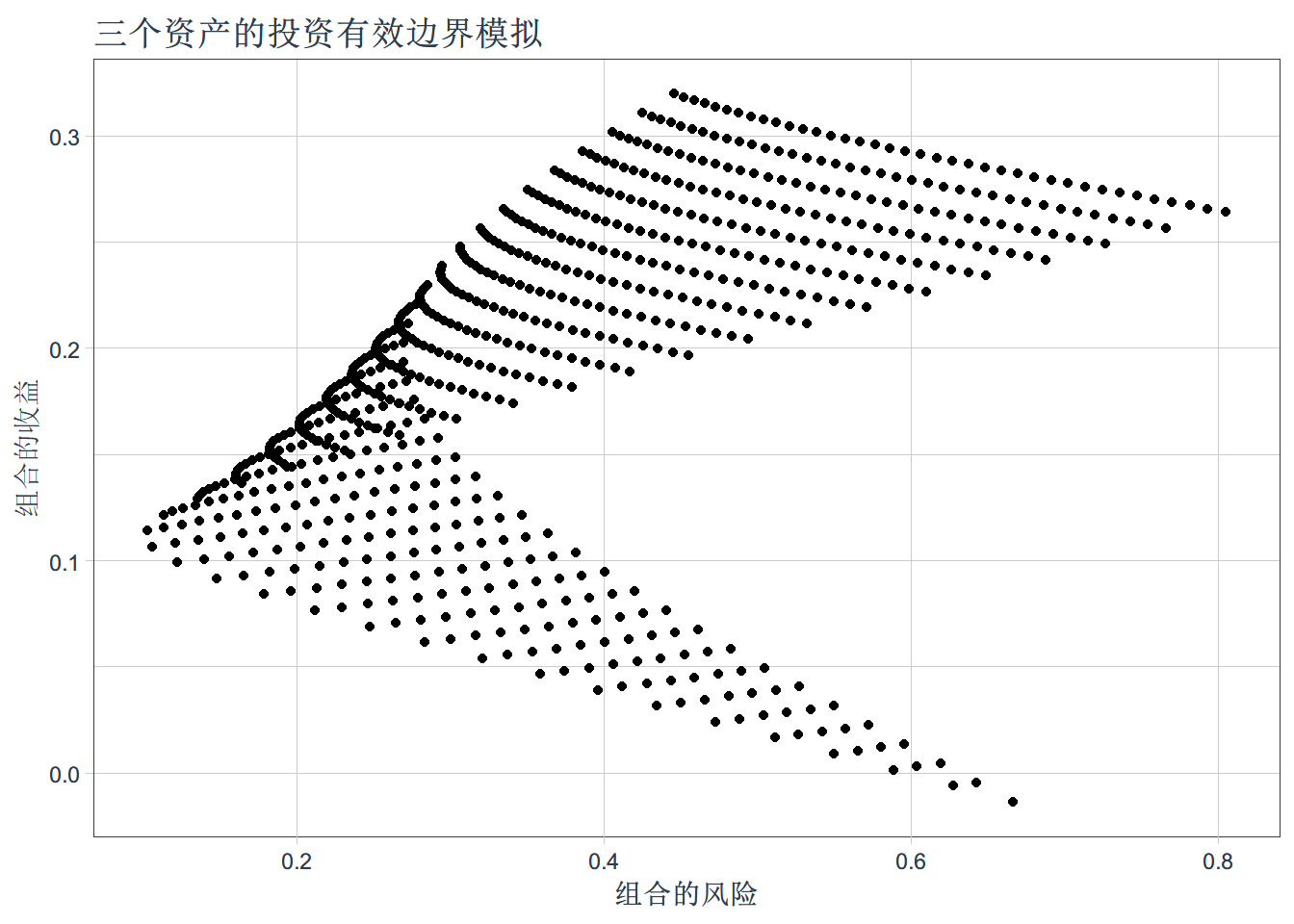
三个资产的思路
- 需要计算(获取)收益矩阵,方差协方差矩阵
- 每改变一次,权重矩阵,就可以得到对应的投资组合的均值和方差
- 将所有的均值-方差组合展现在直角坐标系下
先给定相关参数
ret_m <- matrix(c(0.15,0.12,0.3),nrow=3)
sigma <- matrix(c(0.1,0.02,-0.06,
0.02,0.012,0.07,
-0.06,0.07,0.4),nrow=3) # 3*3我们的目标是随机生成一系列w矩阵生成一堆点
同时我们有一个约束条件,就是要求权重之和等于1
pacman::p_load(gtools,tidyverse)
perms <- permutations(n=50,r=3,seq(-15,15,by = 0.5),repeats.allowed = T)
perms1 <- perms[rowSums(perms) == 10,]
perms1 <- perms1/10
set.seed(123)
my_perms <- perms1[sample(nrow(perms1), 10000, replace=T),]
str(my_perms)## num [1:10000, 1:3] 0.5 0.55 0 0.65 0.05 -0.2 0.25 0.1 0.15 -0.7 ...w <- as_tibble(my_perms)## Warning: The `x` argument of `as_tibble.matrix()` must have column names if `.name_repair` is omitted as of tibble 2.0.0.
## Using compatibility `.name_repair`.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_warnings()` to see where this warning was generated.colnames(w) <- c('w1','w2','w3')
# 生成了1000个满足要求的矩阵
p_ret <- c()
p_sig <- c()
for (i in seq(1,10000)){
p_ret = append(p_ret,as.matrix(w[i,]) %*% ret_m)
p_sig = append(p_sig,sqrt(as.matrix(w[i,]) %*% sigma %*% t(as.matrix(w[i,]))))
}
df <- tibble(p_ret,p_sig)
df <- df %>% drop_na()利用真实A股数据,构建投资有效边界,利用真实数据时,注意剔除那些方差过大的数据,这里限制在1
利用前面讲授的数据进行,添加工商银行作为第四个资产
pacman::p_load(Tushare,tidyverse,tidyquant,DT,plotly,timetk)
api <- pro_api(token = '5adce34e8c81bf7085828754a8e09590c3630032d0f61aad6483eaaa')
bar <- pro_bar(token = '5adce34e8c81bf7085828754a8e09590c3630032d0f61aad6483eaaa')
pingan <- bar(ts_code='601318.SH',start_date="20140101",
end_date='20200407',adj="qfq")## Joining, by = c("ts_code", "trade_date")zgrs <- bar(ts_code='601628.SH',start_date="20140101",
end_date='20200407',adj="qfq")## Joining, by = c("ts_code", "trade_date")zgtb <- bar(ts_code='601601.SH',start_date="20140101",
end_date='20200407',adj="qfq")## Joining, by = c("ts_code", "trade_date")gsyh <- bar(ts_code='601398.SH',start_date="20140101",
end_date='20200407',adj="qfq")## Joining, by = c("ts_code", "trade_date")df <- rbind(pingan,zgrs,zgtb,gsyh)
df <- df %>%
select(ts_code, trade_date,close) %>%
mutate(trade_date = as.Date(trade_date,format="%Y%m%d"),close = as.numeric(close))
df_month_r <- df %>% drop_na() %>%
group_by(ts_code) %>%
tq_transmute (
select = close,
mutate_fun = periodReturn,
period = 'monthly',
col_rename = 'm_returns'
) %>% arrange(trade_date)
return <- df_month_r %>%
group_by(ts_code) %>%
summarise(retrun = mean(m_returns))
return_m <- as.matrix(return[,2])
# 进行数据转换,计算方差协方差矩阵
sigma<-df_month_r %>%
pivot_wider( names_from = ts_code,values_from = m_returns) %>%
timetk::tk_xts(silent = TRUE) %>% # 这一步是强制转换为时间序列数据,同时把ts_code这一列删除掉,
#只保留三个股票的月度收益率,用以方便计算方差协方差矩阵
cov()
p_ret <- c()
p_sig <- c()
for (i in seq(1,2000)){
weight <- rnorm(length(return_m)) ## 随机权重,权重和是否为1
weight <- weight/(sum(weight)) ## 随机权重,权重和是否为1
weight <- matrix(weight,nrow=1) # 转换为矩阵
p_ret = append(p_ret, weight %*% return_m)
p_sig = append(p_sig,sqrt(weight %*% sigma %*% t(weight)))
}
df <- tibble(p_ret,p_sig)
df_p <- df %>%
mutate(p_ret = as.numeric(p_ret),p_sig= as.numeric(p_sig)) %>%
dplyr::filter(p_sig<1)
df_p## # A tibble: 1,924 x 2
## p_ret p_sig
## <dbl> <dbl>
## 1 0.00685 0.0716
## 2 -0.00942 0.139
## 3 0.00163 0.248
## 4 0.0144 0.0854
## 5 0.0114 0.0824
## 6 0.0173 0.0854
## 7 0.0215 0.0938
## 8 0.0150 0.156
## 9 0.00580 0.117
## 10 0.0154 0.0771
## # ... with 1,914 more rowsfig<-ggplot(df_p,aes(p_sig, p_ret)) + geom_point() + tidyquant::theme_tq() +
xlab('组合的风险') + ylab('组合的收益') + ggtitle('四个资产的投资有效边界模拟')
ggplotly(fig,width = 800,height = 500)