使用tidyquant包对高低市盈率分析

张剑

2020/04/01

Categories: 投资学 Tags: 投资 R

上次课留下的思考题

题目思路

  1. 读入数据
  2. 进行数据可视化
  3. 计算日收益率
  4. 简单比较高vs低收市盈率组合是否存在显著差异

首先我们安装tidyquant包，这个包是R做量化投资、金融分析的核心包，我们将大量使用这个包进行分析

这个包的安装方法和其他包一样都是install.packages(“tidyquant”),如果需要安装开发版的同学可以去github上自行学习，相信你们都会用github了，下载开发版肯定不是问题 

# 读入数据，注意目录位置
getwd() #使用这个命令可以知道当前目录的位置，从而定位我们要读入文件的位置
## [1] "D:/github/giteeweb/content/post"
# 使用pacman这个包的好处是帮可以帮我们载入指定包，如果该指定包没有安装，则进行安装
pacman::p_load(tidyverse, tidyquant,readxl,DT)
pe_data <- read_excel("data/pe_data.xls", 
    skip = 2)
colnames(pe_data)<-c("date","pehigh","pelow")
pe_data %>% datatable()
str(pe_data)
## Classes 'tbl_df', 'tbl' and 'data.frame':    2454 obs. of  3 variables:
##  $ date  : POSIXct, format: "2010-03-01" "2010-03-02" ...
##  $ pehigh: num  1226 1223 1239 1198 1201 ...
##  $ pelow : num  5053 5028 5060 4932 4936 ...

我们使用str()函数观察一下数据结构，读入的数据是3列（3个特征），2454个观测值（obs）,第一个特征是时间，第二个是pehigh组指数，第二个是pelow组指数

# 我们使用tidyvers分析流程进行数据转换
# 我们先将第一个日期时间的格式再次转换一下
pe_data <- pe_data %>% mutate(date = as.Date(date,format="%Y-%m-%d"))

目前这个数据结构是所谓的宽数据，接下来把数据转换为所谓的长数据(long)，利用长数据进行作图，我们使用

pe_data_long <- pe_data %>%
  pivot_longer(-date,names_to = "pe_group",values_to = "values")
#使用ggplot进行画图，用颜色区分市盈率高低组
p <- ggplot(pe_data_long,aes(x=date,y=values,color = as.factor(pe_group)))+
              geom_line(size=1.1,alpha=0.6)+ ggtitle("A股市盈率高低组指数2010-2020年") + xlab("时间") + ylab("指数")+
  theme_tq()
# 我们使用了一下plotly包，可以生成交互式的图，这里使用包名加两个冒号调用包中的函数
fig <- plotly::ggplotly(p)
fig
2005201020152000400060008000
pehighpelowA股市盈率高低组指数2010-2020年时间指数as.factor(pe_group)

接下来计算收益率

日收益率计算公式： \[r=\frac{value_t-value_{t-1}}{value_{t-1}}\]
### 计算日收益率

我们直接利用包计算日收益率，先参看包能给我们做什么,我们使用tidyquant包下面的tq_transmute集成函数进行，主要使用其中的“dailyReturn” , “monthlyReturn”, “yearlyReturn” 进行展示，tq_tansmute函数具体帮助地址：这里

tq_transmute_fun_options()
## $zoo
##  [1] "rollapply"          "rollapplyr"         "rollmax"           
##  [4] "rollmax.default"    "rollmaxr"           "rollmean"          
##  [7] "rollmean.default"   "rollmeanr"          "rollmedian"        
## [10] "rollmedian.default" "rollmedianr"        "rollsum"           
## [13] "rollsum.default"    "rollsumr"          
## 
## $xts
##  [1] "apply.daily"     "apply.monthly"   "apply.quarterly" "apply.weekly"   
##  [5] "apply.yearly"    "diff.xts"        "lag.xts"         "period.apply"   
##  [9] "period.max"      "period.min"      "period.prod"     "period.sum"     
## [13] "periodicity"     "to.daily"        "to.hourly"       "to.minutes"     
## [17] "to.minutes10"    "to.minutes15"    "to.minutes3"     "to.minutes30"   
## [21] "to.minutes5"     "to.monthly"      "to.period"       "to.quarterly"   
## [25] "to.weekly"       "to.yearly"       "to_period"      
## 
## $quantmod
##  [1] "allReturns"      "annualReturn"    "ClCl"            "dailyReturn"    
##  [5] "Delt"            "HiCl"            "Lag"             "LoCl"           
##  [9] "LoHi"            "monthlyReturn"   "Next"            "OpCl"           
## [13] "OpHi"            "OpLo"            "OpOp"            "periodReturn"   
## [17] "quarterlyReturn" "seriesAccel"     "seriesDecel"     "seriesDecr"     
## [21] "seriesHi"        "seriesIncr"      "seriesLo"        "weeklyReturn"   
## [25] "yearlyReturn"   
## 
## $TTR
##  [1] "adjRatios"          "ADX"                "ALMA"              
##  [4] "aroon"              "ATR"                "BBands"            
##  [7] "CCI"                "chaikinAD"          "chaikinVolatility" 
## [10] "CLV"                "CMF"                "CMO"               
## [13] "DEMA"               "DonchianChannel"    "DPO"               
## [16] "DVI"                "EMA"                "EMV"               
## [19] "EVWMA"              "GMMA"               "growth"            
## [22] "HMA"                "KST"                "lags"              
## [25] "MACD"               "MFI"                "momentum"          
## [28] "OBV"                "PBands"             "ROC"               
## [31] "rollSFM"            "RSI"                "runCor"            
## [34] "runCov"             "runMAD"             "runMax"            
## [37] "runMean"            "runMedian"          "runMin"            
## [40] "runPercentRank"     "runSD"              "runSum"            
## [43] "runVar"             "SAR"                "SMA"               
## [46] "SMI"                "SNR"                "stoch"             
## [49] "TDI"                "TRIX"               "ultimateOscillator"
## [52] "VHF"                "VMA"                "volatility"        
## [55] "VWAP"               "VWMA"               "wilderSum"         
## [58] "williamsAD"         "WMA"                "WPR"               
## [61] "ZigZag"             "ZLEMA"             
## 
## $PerformanceAnalytics
## [1] "Return.annualized"        "Return.annualized.excess"
## [3] "Return.clean"             "Return.cumulative"       
## [5] "Return.excess"            "Return.Geltner"          
## [7] "zerofill"
pe_data_return <- pe_data_long %>% drop_na() %>%
  group_by(pe_group) %>%
  tq_transmute(select = values,
               mutate_fun = dailyReturn)
str(pe_data_return)
## Classes 'grouped_df', 'tbl_df', 'tbl' and 'data.frame':  4904 obs. of  3 variables:
##  $ pe_group     : chr  "pehigh" "pehigh" "pehigh" "pehigh" ...
##  $ date         : Date, format: "2010-03-01" "2010-03-02" ...
##  $ daily.returns: num  0 -0.00167 0.01301 -0.03375 0.0032 ...
##  - attr(*, "groups")=Classes 'tbl_df', 'tbl' and 'data.frame':   2 obs. of  2 variables:
##   ..$ pe_group: chr  "pehigh" "pelow"
##   ..$ .rows   :List of 2
##   .. ..$ : int  1 2 3 4 5 6 7 8 9 10 ...
##   .. ..$ : int  2453 2454 2455 2456 2457 2458 2459 2460 2461 2462 ...
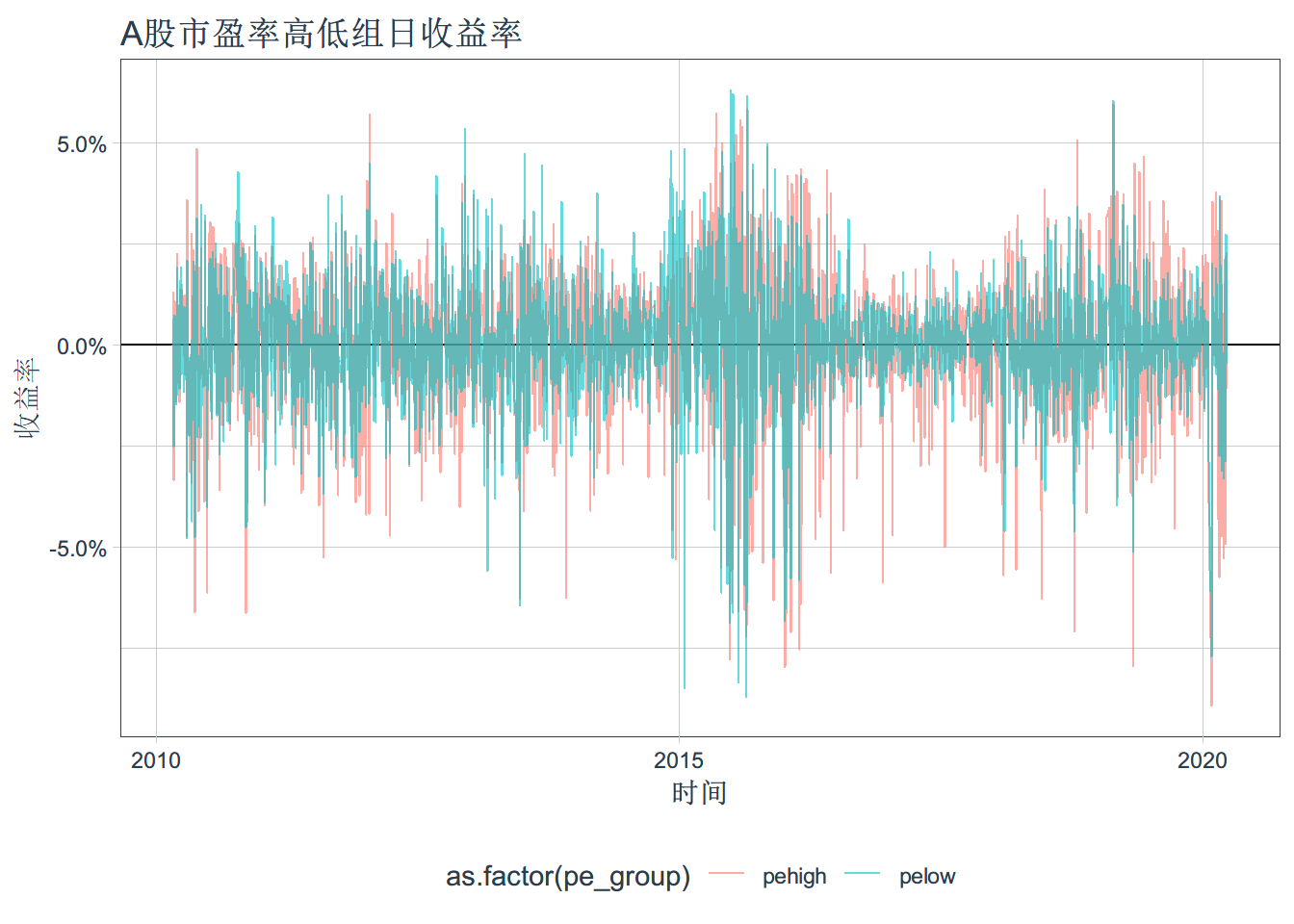
##   ..- attr(*, ".drop")= logi FALSE
ggplot(pe_data_return,aes(x=date, y=daily.returns, color = as.factor(pe_group)))+
  scale_y_continuous(labels = scales::percent)+geom_hline(yintercept = 0)+
              geom_line(alpha=0.6)+ ggtitle("A股市盈率高低组日收益率") + xlab("时间") + ylab("收益率")+
  theme_tq()

计算季度收益率

我们直接利用tidyquant包计算季度收益率

pe_data_return_q <- pe_data_long %>% drop_na() %>%
  group_by(pe_group) %>%
  tq_transmute(select = values,
               mutate_fun = quarterlyReturn)
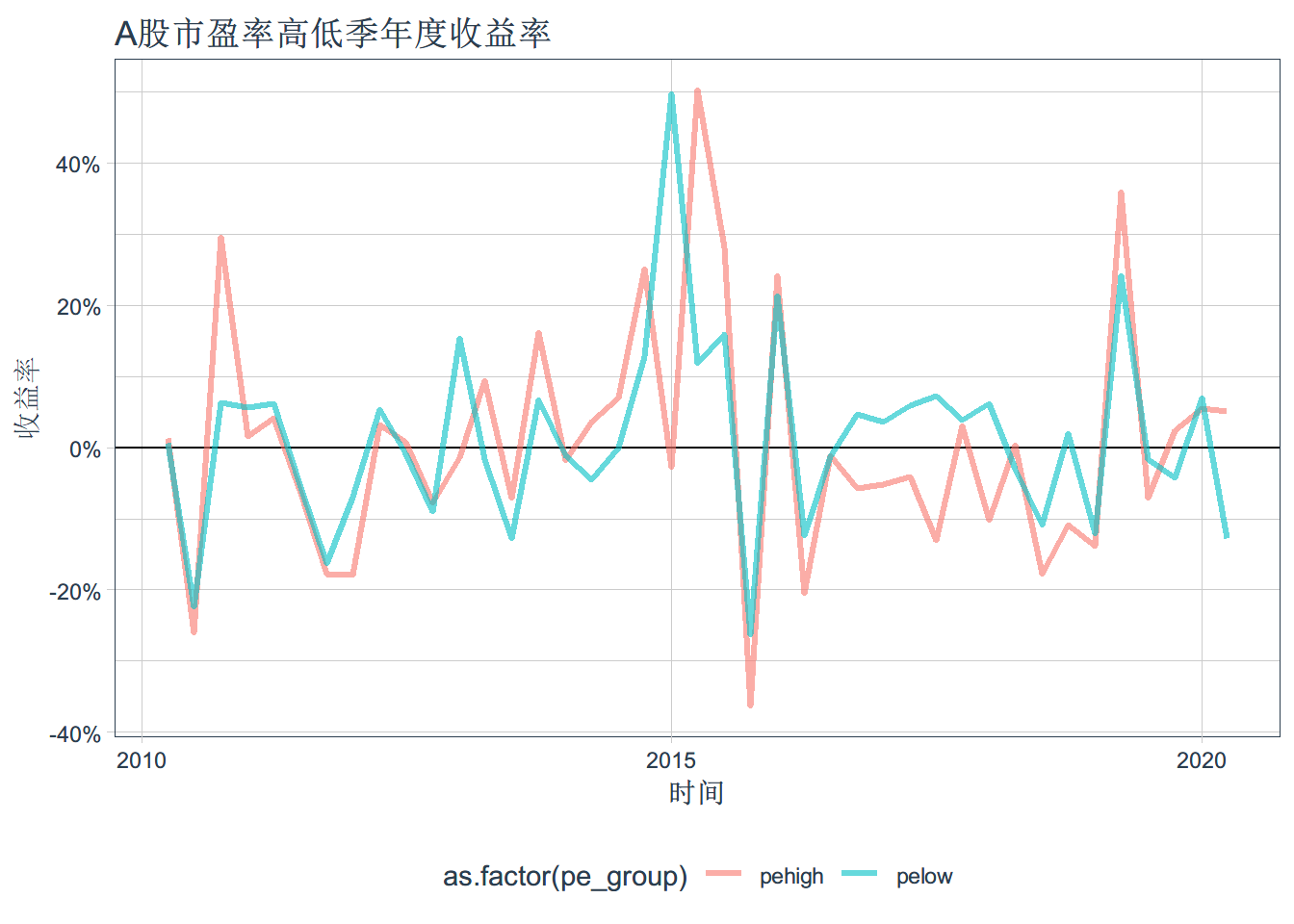
ggplot(pe_data_return_q,aes(x=date, y=quarterly.returns, color = as.factor(pe_group)))+
  scale_y_continuous(labels = scales::percent)+geom_hline(yintercept = 0)+
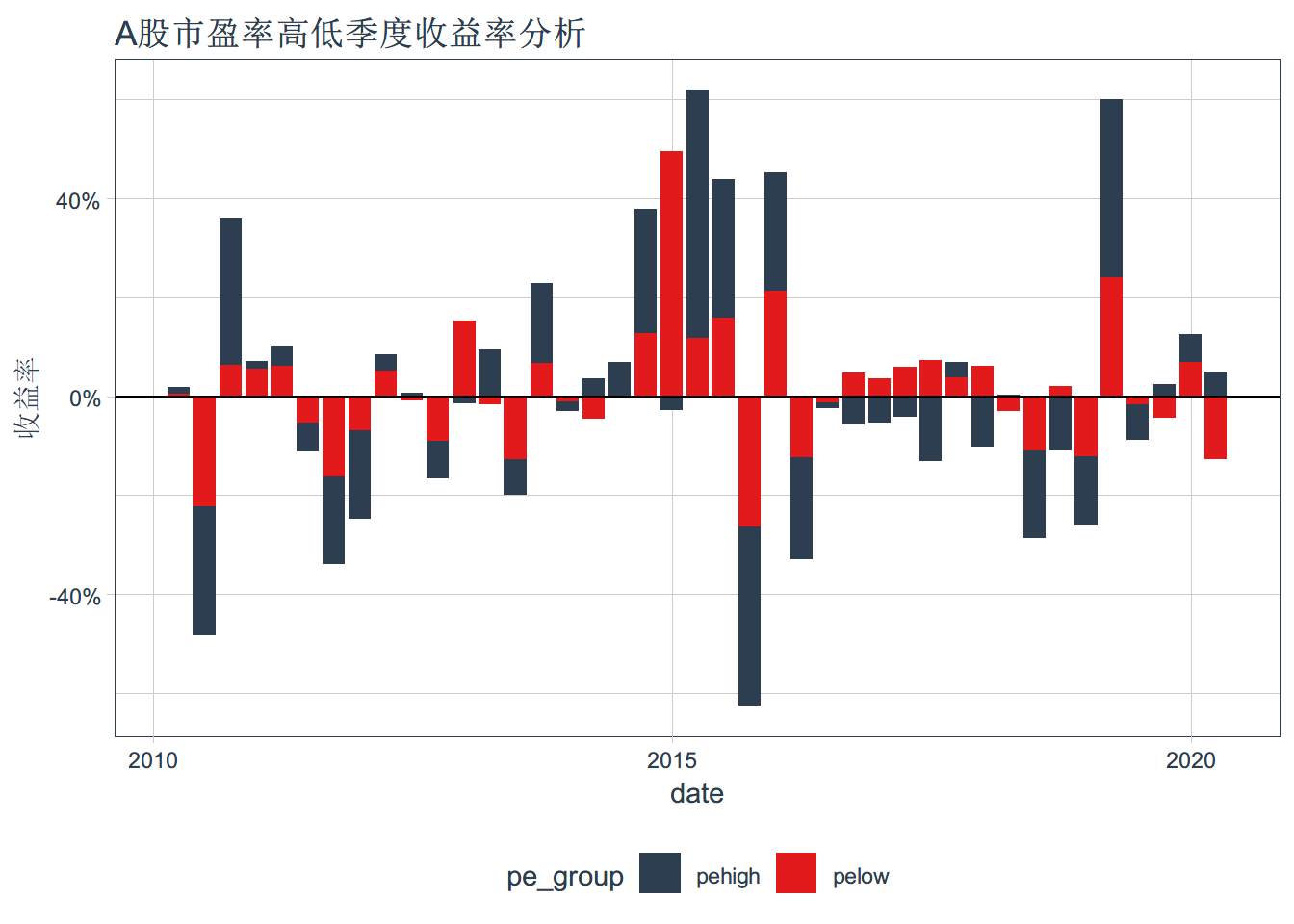
              geom_line(size= 1.1,alpha=0.6)+ ggtitle("A股市盈率高低季年度收益率") + xlab("时间") + ylab("收益率")+  theme_tq()

ggplot(pe_data_return_q,aes(x=date,y=quarterly.returns,fill=pe_group))+  geom_col()+geom_hline(yintercept = 0)+
   scale_y_continuous(labels = scales::percent) +theme_tq()+ scale_fill_tq()+ggtitle("A股市盈率高低季度收益率分析") + ylab("收益率")

计算年度收益

pe_data_return_y <- pe_data_long %>% drop_na() %>%
  group_by(pe_group) %>%
  tq_transmute(select = values,
               mutate_fun = yearlyReturn)
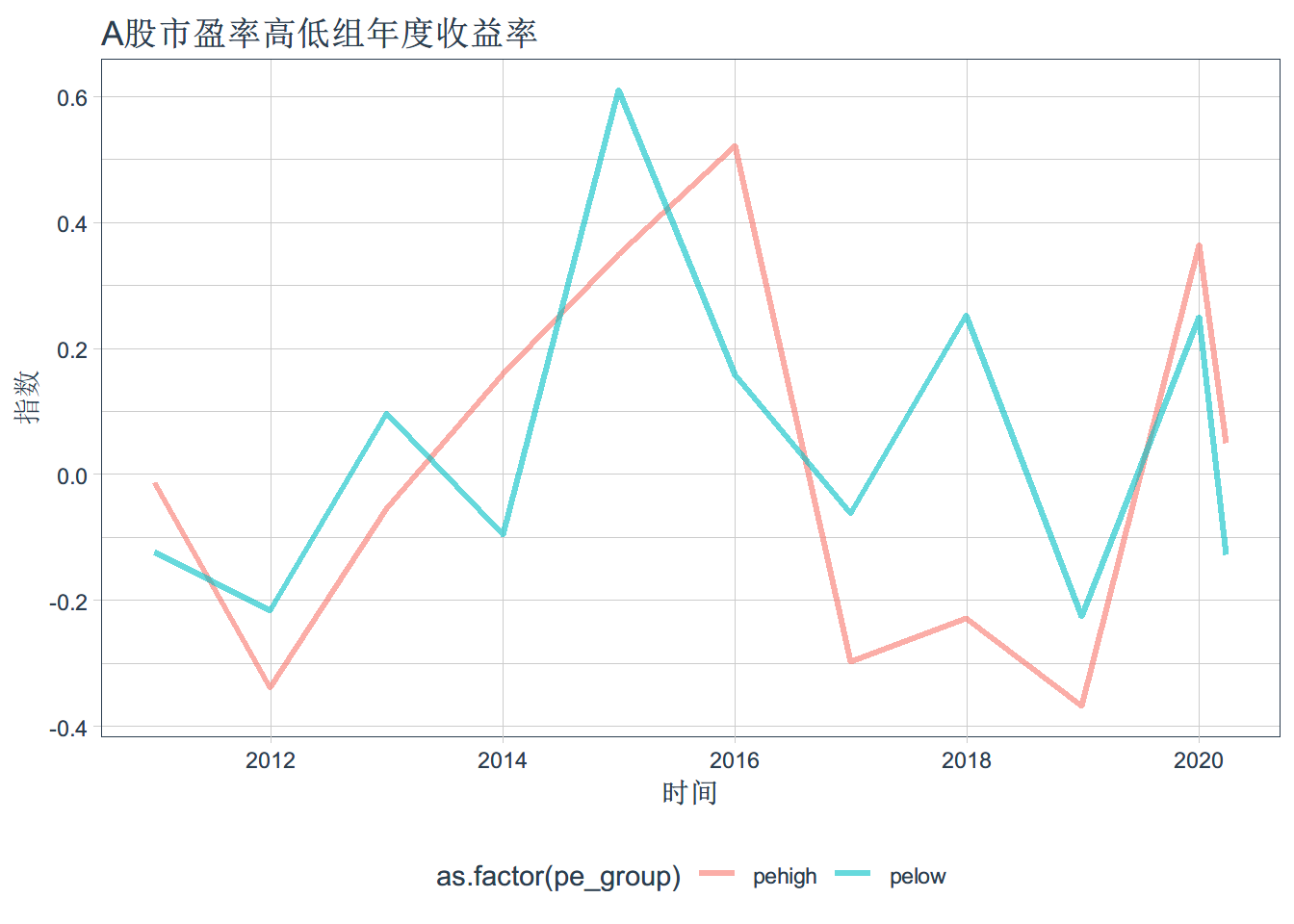
ggplot(pe_data_return_y,aes(x=date, y=yearly.returns, color = as.factor(pe_group)))+
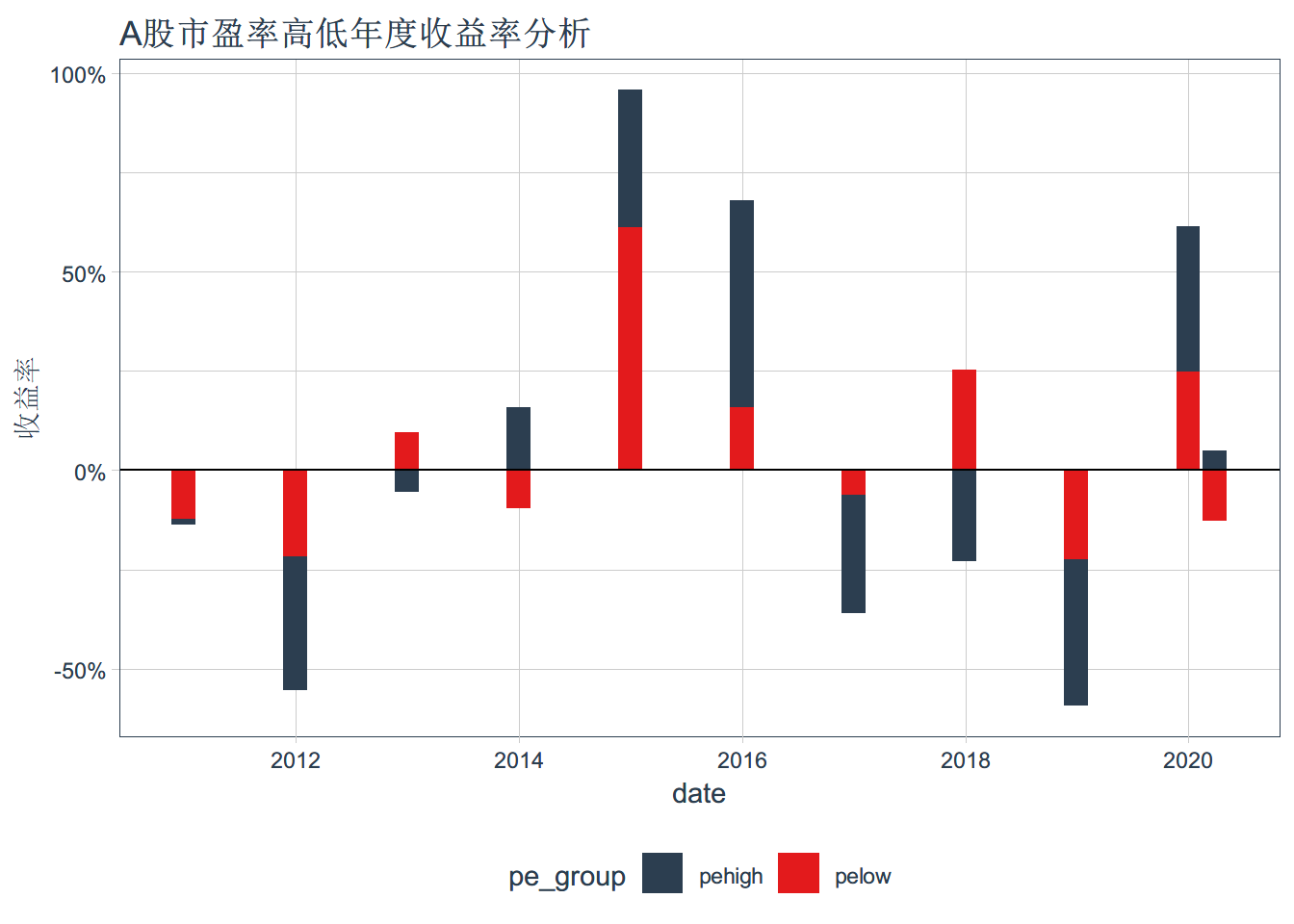
              geom_line(size= 1.1,alpha=0.6)+ ggtitle("A股市盈率高低组年度收益率") + xlab("时间") + ylab("指数")+  theme_tq()

ggplot(pe_data_return_y,aes(x=date,y=yearly.returns,fill=pe_group))+  geom_col()+geom_hline(yintercept = 0)+
   scale_y_continuous(labels = scales::percent) +theme_tq()+ scale_fill_tq()+
  ggtitle("A股市盈率高低年度收益率分析") + ylab("收益率")

组间差异判断

接下来，我们分析一下是否高低市盈率组投资组合是存在显著差异，我们这里就只比高低组PE较全部样本

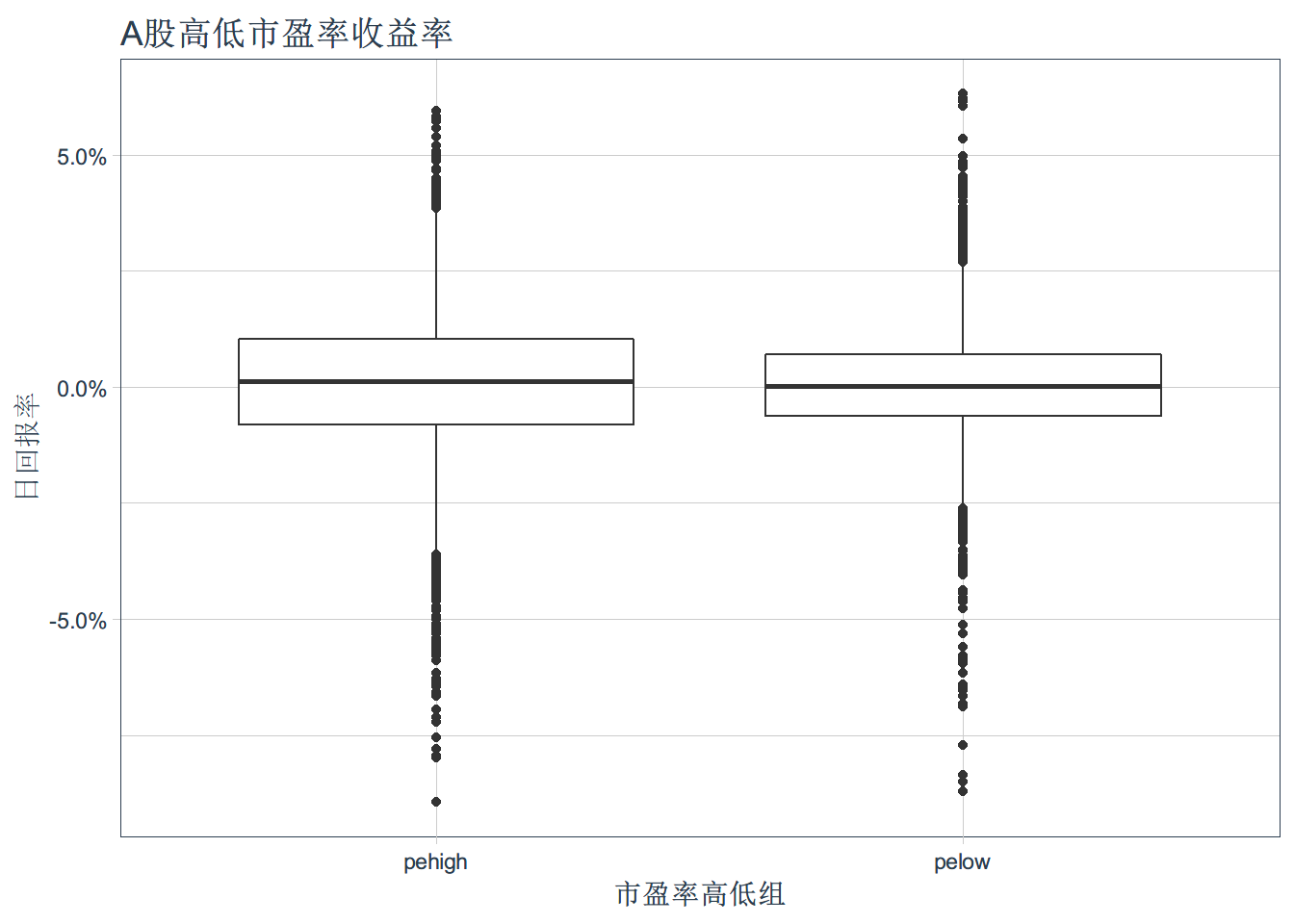
ggplot(pe_data_return,aes(x=pe_group,y=daily.returns))+
   scale_y_continuous(labels = scales::percent) +
  geom_boxplot() + theme_tq() +
  ggtitle("A股高低市盈率收益率") + xlab("市盈率高低组") + ylab("日回报率")

t.test(daily.returns ~ pe_group, data = pe_data_return, paired = TRUE)
## 
##  Paired t-test
## 
## data:  daily.returns by pe_group
## t = -0.65314, df = 2451, p-value = 0.5137
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -0.0006873786  0.0003438866
## sample estimates:
## mean of the differences 
##            -0.000171746

如果大家能看到统计分析，可以发现市盈率高的投资组合与市盈率低的投资组合，它们的日收益率不存在明显的差异。

有兴趣的同学，可以按年度划分，看看牛市和熊市期间是否存在差异。