Bond Valuation

张剑

2020/03/21

Categories: 投资学 Tags: R

债券估值基础

假设债券的现金流如下：投资面值为100元，票面利率为5％，到期日为5年的债券。

息票利率是您从持有债券中获得的利息，因此，在债券到期之前，每年将获得5美元的息票付款。到期时，您还将获得100的面值返还。

计算每个现金流量的现值

计算债券的价值

假设我们给定该债券的到期收益率为6%

# 先调入包
library(tidyverse)
library(ggthemes) # ggplot2的主题包
library(ggfortify)

cf <- c(5,5,5,5,105)
cf_df <- as_tibble(cf)
## Warning: Calling `as_tibble()` on a vector is discouraged, because the behavior is likely to change in the future. Use `tibble::enframe(name = NULL)` instead.
## This warning is displayed once per session.
# 生成一个时间序列
cf_df <- cf_df %>%
  mutate(year = as.numeric(rownames(cf_df))) %>%
  rename(cf = value)
cf_df
## # A tibble: 5 x 2
##      cf  year
##   <dbl> <dbl>
## 1     5     1
## 2     5     2
## 3     5     3
## 4     5     4
## 5   105     5
# 继续生成一个每一期的现金流的现值
cf_df <- cf_df %>%
  mutate(pv = cf/(1+0.06)^year)
cf_df
## # A tibble: 5 x 3
##      cf  year    pv
##   <dbl> <dbl> <dbl>
## 1     5     1  4.72
## 2     5     2  4.45
## 3     5     3  4.20
## 4     5     4  3.96
## 5   105     5 78.5
sum(cf_df$pv)
## [1] 95.78764

以上是我们分步计算得到的结果，接下来我们尝试把上面的内容写成一个函数

一个函数需要给定一些参数：

  • p —— 面值
  • r —— coupon rate（票息率）
  • t —— 到期时间 time to maturity
  • y —— 该债券的到期收益率

最基本的债券定价

bond_val <- function(p=100,r,t,y) {
  cf <- c(rep(p*r,t-1),p*(1+r))
  cf_df <- as_tibble(cf)
  cf_df <- cf_df %>%
  mutate(year = as.numeric(rownames(cf_df))) %>%
  rename(cf = value)
  cf_df <- cf_df %>%
  mutate(pv = cf/(1+y)^year)
  return(sum(cf_df$pv))
}
bond_val(r=0.01,t=10,y=0.03)
## [1] 82.93959

模拟

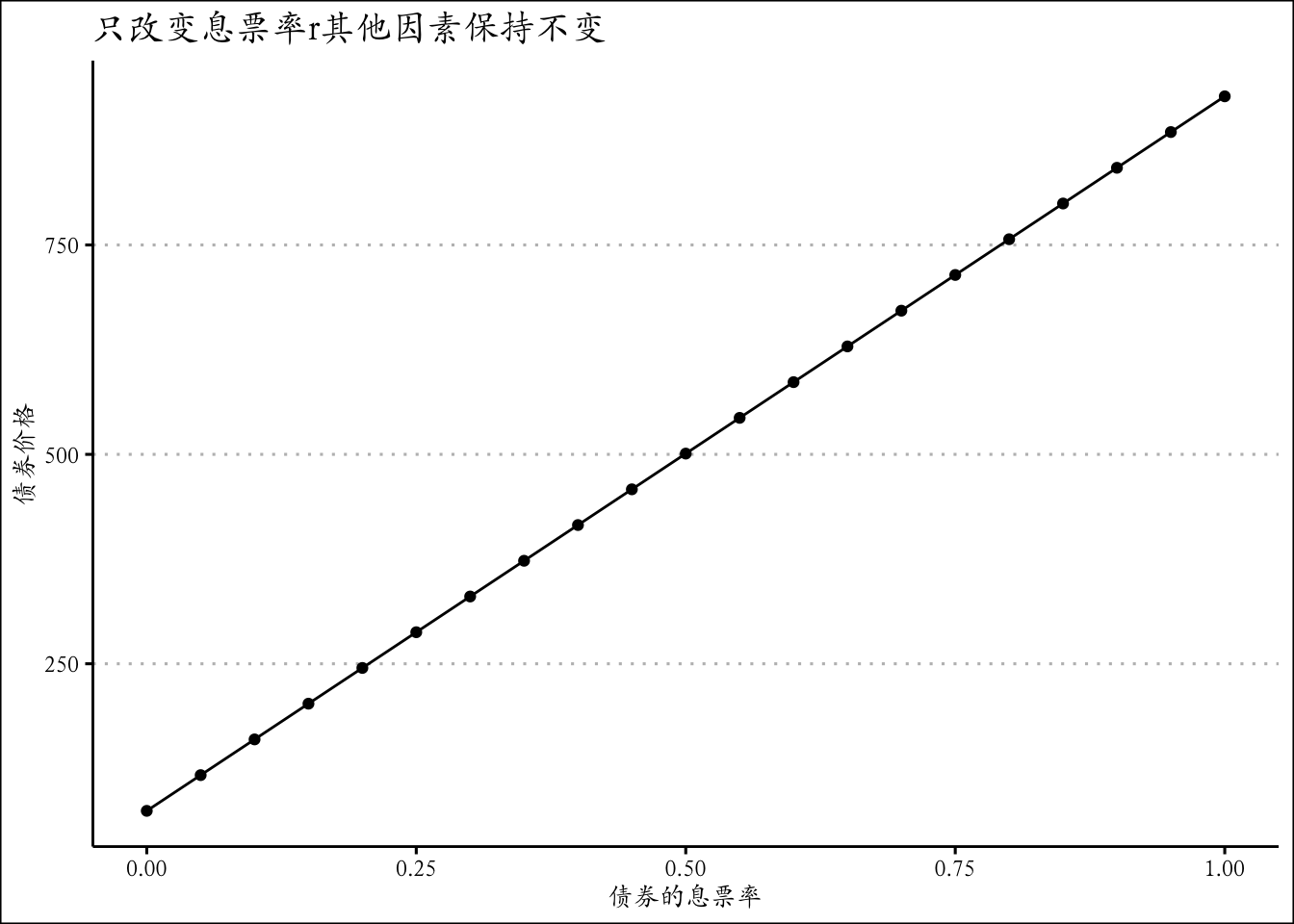
展示保持其他因素不变，只改变r,t,y中一个，债券价格变化

# 首先保持其他不变只改变息票率，其他的类似
sim_bond <- NULL
for (i in seq(0,1,by=0.05)){
  sim_bond <- c(sim_bond,bond_val(r=i,t=10,y=0.03))
}
df <- tibble(bond_v = sim_bond,r=seq(0,1,by=0.05))
ggplot(df,mapping = aes(x=r,y=bond_v))+  geom_point()+
         geom_line() + theme_clean()+ggtitle('只改变息票率r其他因素保持不变')+
  xlab("债券的息票率") + ylab('债券价格')+theme(text = element_text(family='Kai'))

#依葫芦画瓢
sim_bond <- NULL
for (i in seq(0,1,by=0.05)){
  sim_bond <- c(sim_bond,bond_val(r=0.05,t=10,y=i))
}
df <- tibble(bond_v = sim_bond,y=seq(0,1,by=0.05))
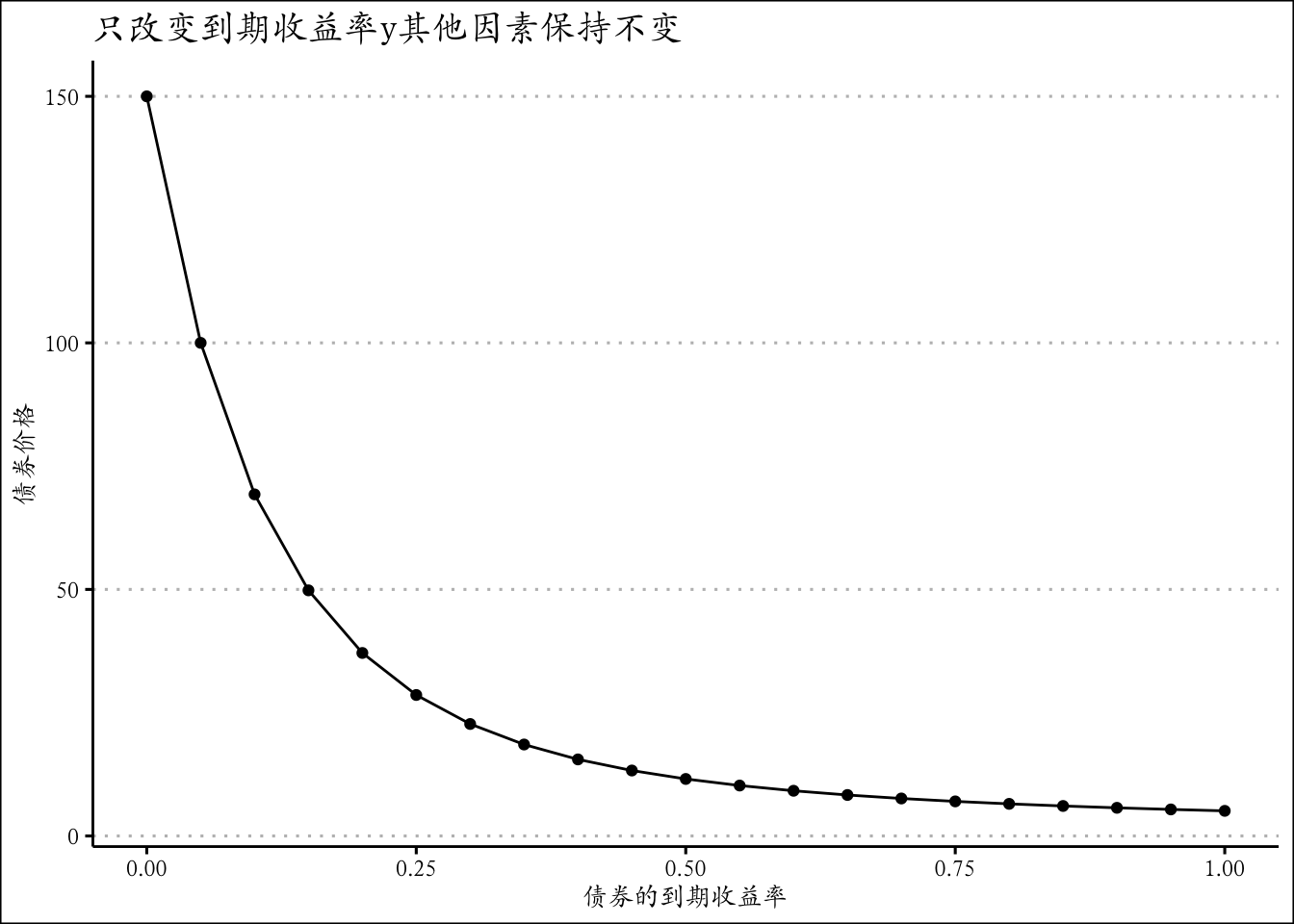
ggplot(df,mapping = aes(x=y,y=bond_v))+ geom_point()+
         geom_line() + theme_clean()+ggtitle('只改变到期收益率y其他因素保持不变')+
  xlab("债券的到期收益率") + ylab('债券价格')+theme(text = element_text(family='Kai'))

#依葫芦画瓢2
sim_bond <- NULL
for (i in seq(1,30,by=1)){
  sim_bond <- c(sim_bond,bond_val(r=0.05,t=i,y=0.03))
}
df <- tibble(bond_v = sim_bond,t=seq(1,30,by=1))
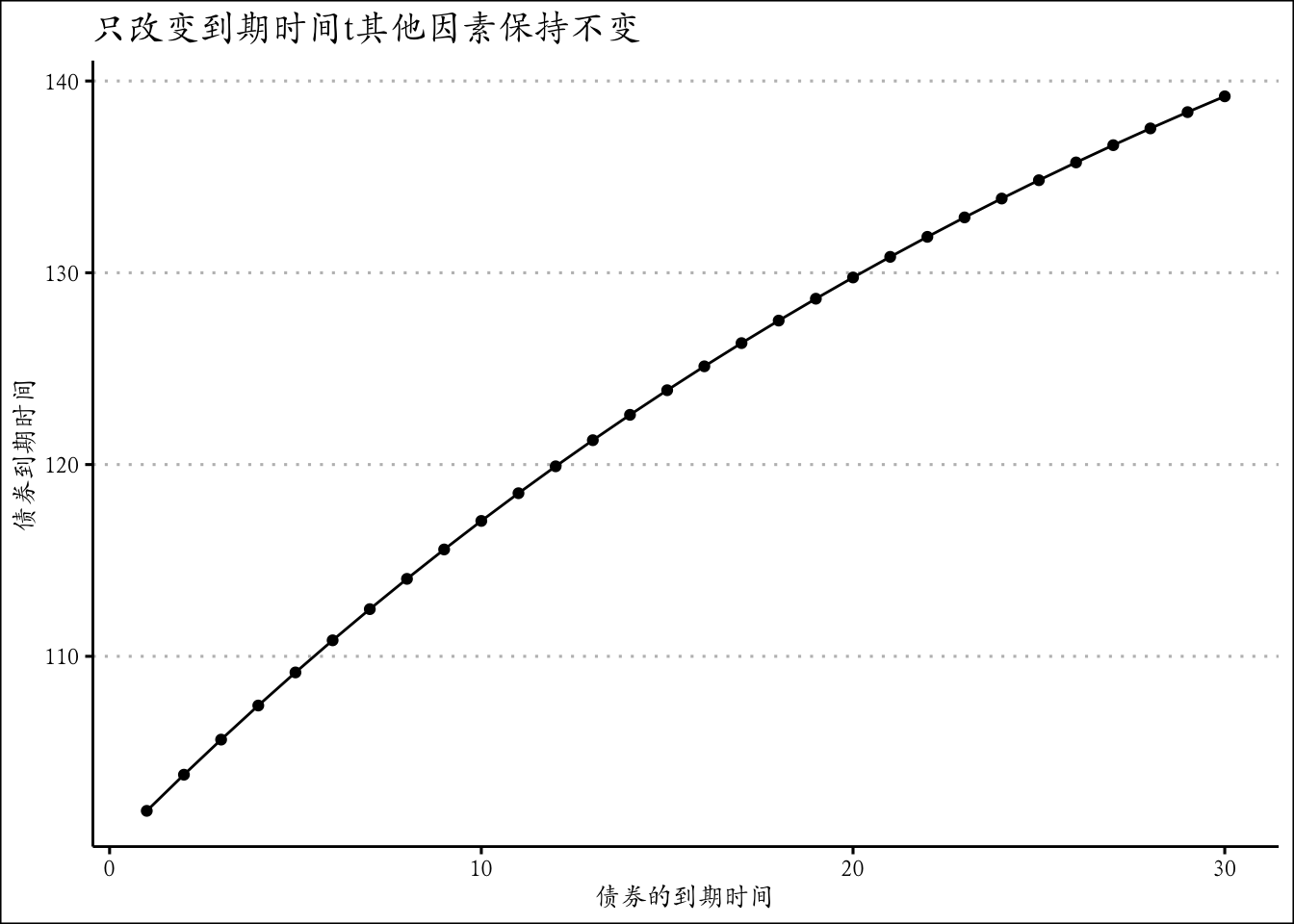
ggplot(df,mapping = aes(x=t,y=bond_v))+ geom_point()+
         geom_line() + theme_clean()+ggtitle('只改变到期时间t其他因素保持不变')+
  xlab("债券的到期时间") + ylab('债券到期时间')+theme(text = element_text(family='Kai'))

什么决定了债券的yield？

各种因素对债券价格的影响

到期收益率变化对债券价格的影响

微小的变化（上升、或下降）对债券价格的影响是对称的

如果比较大的yield变化对债券价格的影响是非对称的

# 继续利用我们上面写的函数进行演示
c_1 <- bond_val(r=0.1,t=10,y=0.101)/bond_val(r=0.1,t=10,y=0.1)-1
c_2 <- bond_val(r=0.1,t=10,y=0.099)/bond_val(r=0.1,t=10,y=0.1)-1
paste("到期收益率上涨时价格变化%",c_1)
## [1] "到期收益率上涨时价格变化% -0.00611825929117416"
paste("到期收益率下降时价格变化%",c_2)
## [1] "到期收益率下降时价格变化% 0.00617105235319015"
#当到期收益率变化较大时
c_3 <- bond_val(r=0.1,t=10,y=0.14)/bond_val(r=0.1,t=10,y=0.1)-1
c_4 <- bond_val(r=0.1,t=10,y=0.06)/bond_val(r=0.1,t=10,y=0.1)-1
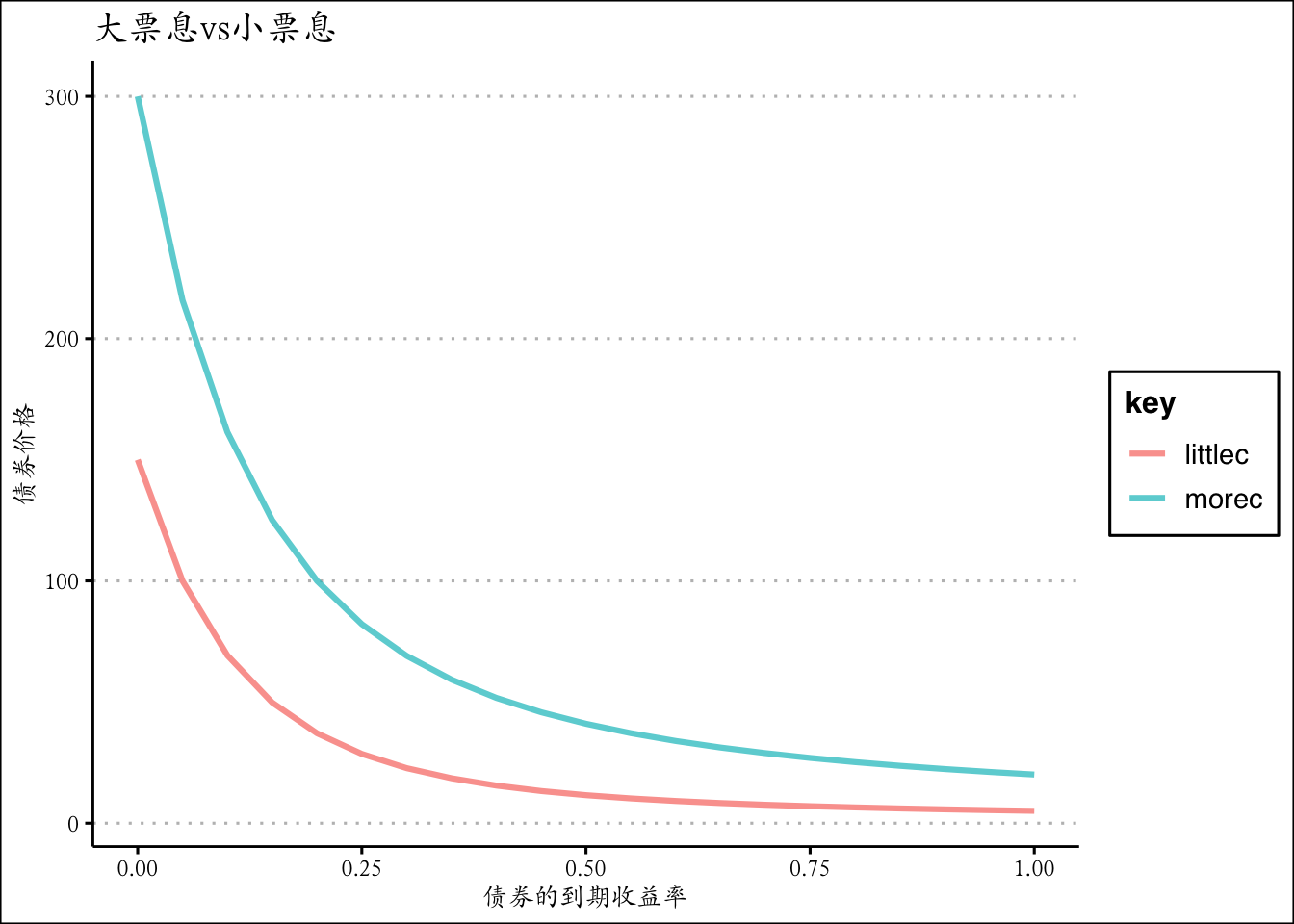
paste("到期收益率上涨时价格变化%",c_3)
## [1] "到期收益率上涨时价格变化% -0.208644625851743"
paste("到期收益率下降时价格变化%",c_4)
## [1] "到期收益率下降时价格变化% 0.294403482056588"

票息率越低，债券变异性更大（敏感性越强），受到到期收益率的影响越大

c_5 <- bond_val(r=0.1,t=20,y=0.08)/bond_val(r=0.1,t=20,y=0.1)-1
c_6 <- bond_val(r=0.05,t=20,y=0.08)/bond_val(r=0.05,t=20,y=0.1)-1
c_7 <- bond_val(r=0,t=20,y=0.08)/bond_val(r=0,t=20,y=0.1)-1
paste("大票息债券的变化%",c_5)
## [1] "大票息债券的变化% 0.196362948148986"
paste("小票息债券的变化%",c_6)
## [1] "小票息债券的变化% 0.228328021964517"
paste("零息债券的变化%",c_7)
## [1] "零息债券的变化% 0.44337305443869"
#依葫芦画瓢
sim_bond <- NULL
for (i in seq(0,1,by=0.05)){
  sim_bond <- c(sim_bond,bond_val(r=0.05,t=10,y=i))
}
sim_bond_2 <- NULL
for (i in seq(0,1,by=0.05)){
  sim_bond_2 <- c(sim_bond_2,bond_val(r=0.2,t=10,y=i))
}


df <- tibble(littlec = sim_bond,morec=sim_bond_2, y=seq(0,1,by=0.05)) %>%
  gather(key = 'key',value='value',-y)

ggplot(df,aes(x=y,y=value,color=key),size=1.1,alpha=0.7) +
  geom_line(size=1.1,alpha=0.7)+ggtitle('大票息vs小票息')+
  xlab("债券的到期收益率") + ylab('债券价格')+theme_clean()+
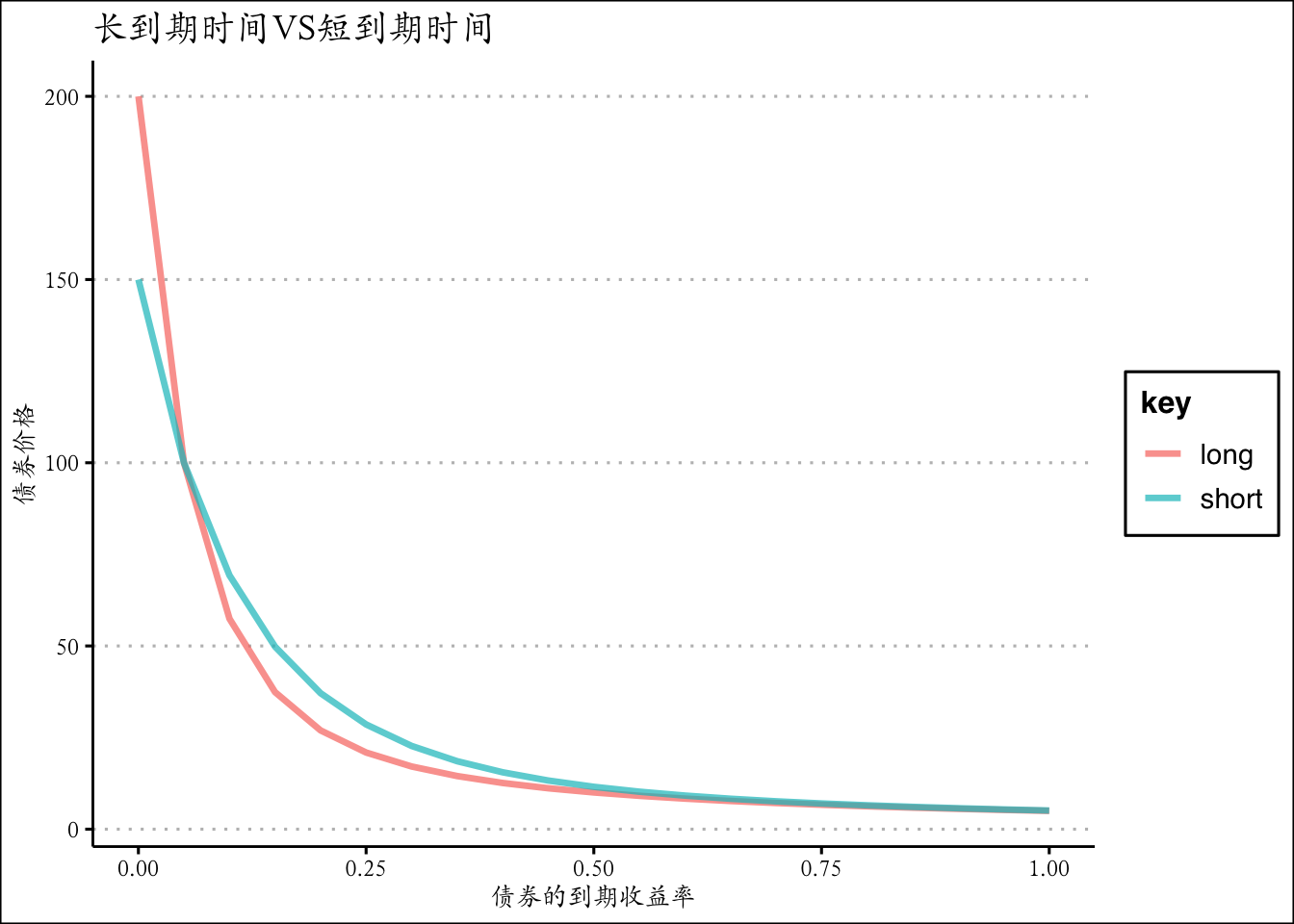
  theme(text = element_text(family='Kai'))

更长的到期时间，债券变异性更大（敏感性越强），收到到期收益率的影响越大

bond_val(r=0.1,t=20,y=0.08)/bond_val(r=0.1,t=20,y=0.1)-1
## [1] 0.1963629
bond_val(r=0.1,t=10,y=0.08)/bond_val(r=0.1,t=10,y=0.1)-1
## [1] 0.1342016
#依葫芦画瓢3
short <- NULL
for (i in seq(0,1,by=0.05)){
  short <- c(short,bond_val(r=0.05,t=10,y=i))
}
long <- NULL
for (i in seq(0,1,by=0.05)){
  long <- c(long,bond_val(r=0.05,t=20,y=i))
}


df <- tibble(short = short,long=long, y=seq(0,1,by=0.05)) %>%
  gather(key = 'key',value='value',-y)

ggplot(df,aes(x=y,y=value,color=key),size=1.2,alpha=0.7) +
  geom_line(size=1.2,alpha=0.7)+ggtitle('长到期时间VS短到期时间')+
  xlab("债券的到期收益率") + ylab('债券价格')+theme_clean()+
  theme(text = element_text(family='Kai'))

债券的久其

公式和定义ppt上已经写好了，我们直接来写function

mac_dur <- function(p=100,r,t,y) {
  cf <- c(rep(p*r,t-1),p*(1+r))
  
  cf_df <- as_tibble(cf)
  
  cf_df <- cf_df %>%
  mutate(year = as.numeric(rownames(cf_df))) %>%
  rename(cf = value)
  
  cf_df <- cf_df %>%
  mutate(pv = cf/(1+y)^year) %>%
    mutate(total_pv = year*cf/(1+y)^year)
  
  return(sum(cf_df$total_pv)/sum(cf_df$pv))
}

dur_1 <-mac_dur(r=0.1,t=20,y=0.08)
dur_2 <- mac_dur(r=0.3,t=10,y=0.06)

paste("小票息债券的久其是:",dur_1)
## [1] "小票息债券的久其是: 10.1823263432589"
paste("大票息债券的久其是:",dur_2)
## [1] "大票息债券的久其是: 6.02680175748431"
if (dur_2<dur_1){
  print('dur_2债券的易变性（敏感性）更弱')
}else(print('dur_2债券的易变性更强'))
## [1] "dur_2债券的易变性（敏感性）更弱"

继续构建修正久其，修正久其就是在麦考利久其的基础上除以(1+y)

re_dur <- function(p=100,r,t,y) {
  cf <- c(rep(p*r,t-1),p*(1+r))
  
  cf_df <- as_tibble(cf)
  
  cf_df <- cf_df %>%
  mutate(year = as.numeric(rownames(cf_df))) %>%
  rename(cf = value)
  
  cf_df <- cf_df %>%
  mutate(pv = cf/(1+y)^year) %>%
    mutate(total_pv = year*cf/(1+y)^year)
  
  dur = sum(cf_df$total_pv)/sum(cf_df$pv)
  
  re_dur = dur/(1+y)
  return(re_dur)
}

使用JrvFiance包计算现金流的久期、债券价格

library(jrvFinance)
library(tidyverse)
# jrvFiance包中的duration函数可以计算现金流的久期
mac_d <- duration(cf = c(200,300,10000),rate = 5e-2) # 麦考利久期
md_d <- duration(cf = c(200,300,10000),rate = 5e-2,modified = T) #修正久期
md_d == mac_d/(1+5e-2) #检验一下修正久期是否等于麦考利久期除以（1+y)
## [1] TRUE
print(list(mac_d,md_d))
## [[1]]
## [1] 2.928243
## 
## [[2]]
## [1] 2.788802
## 接下来计算债券价格，之前我们写了自己的函数，现在我们直接使用包里的函数
#该函数为bond.price() settle 结算日 mature 到期日，注意这两个一定要用字符串，或者日期型格式
#coupon和yield大家可以理解
bond.price(settle="2018-03-15", mature="2023-03-15", coupon=5e-2,
           yield=6e-2)
## [1] 95.7349
bond.price(settle="2018-03-15", mature="2023-03-15", coupon=0,
           yield=6e-2)
## [1] 74.40939
# freq控制coupon支付频率1是年支付，2是半年一次，12是月度
bond.price(settle="2012-04-15", mature="2022-01-01", coupon=5e-2,
           yield=6e-2, freq=12)
## [1] 92.65338
#comp.freq 复利的频率方法还是同上
bond.price(settle="2012-04-15", mature="2022-01-01", coupon=5e-2,
           yield=6e-2, freq=12, comp.freq = 2)
## [1] 93.17233

使用JrvFiance包计算债券duration

library(ggfortify)
ggthemr:: ggthemr('dust') #这也是一种调用包里面函数的方法，我这里调用了ggthemr颜色包里面的dust色板

bond.duration(settle="2018-03-15", mature="2023-03-15", coupon=5e-2,
           yield=6e-2)
## [1] 4.471679
bond.duration(settle="2018-03-15", mature="2023-03-15", coupon=3e-2,
           yield=6e-2)
## [1] 4.652
sim_dur <- NULL
for (i in seq(0,0.2,by=0.01)){
sim_dur <- c(sim_dur,duration= bond.duration(settle="2018-03-15", mature="2023-03-15", coupon=i,
           yield=6e-2,modified = T))
}

df <- tibble(coup =seq(0,0.2,by=0.01),sim_dur=sim_dur )
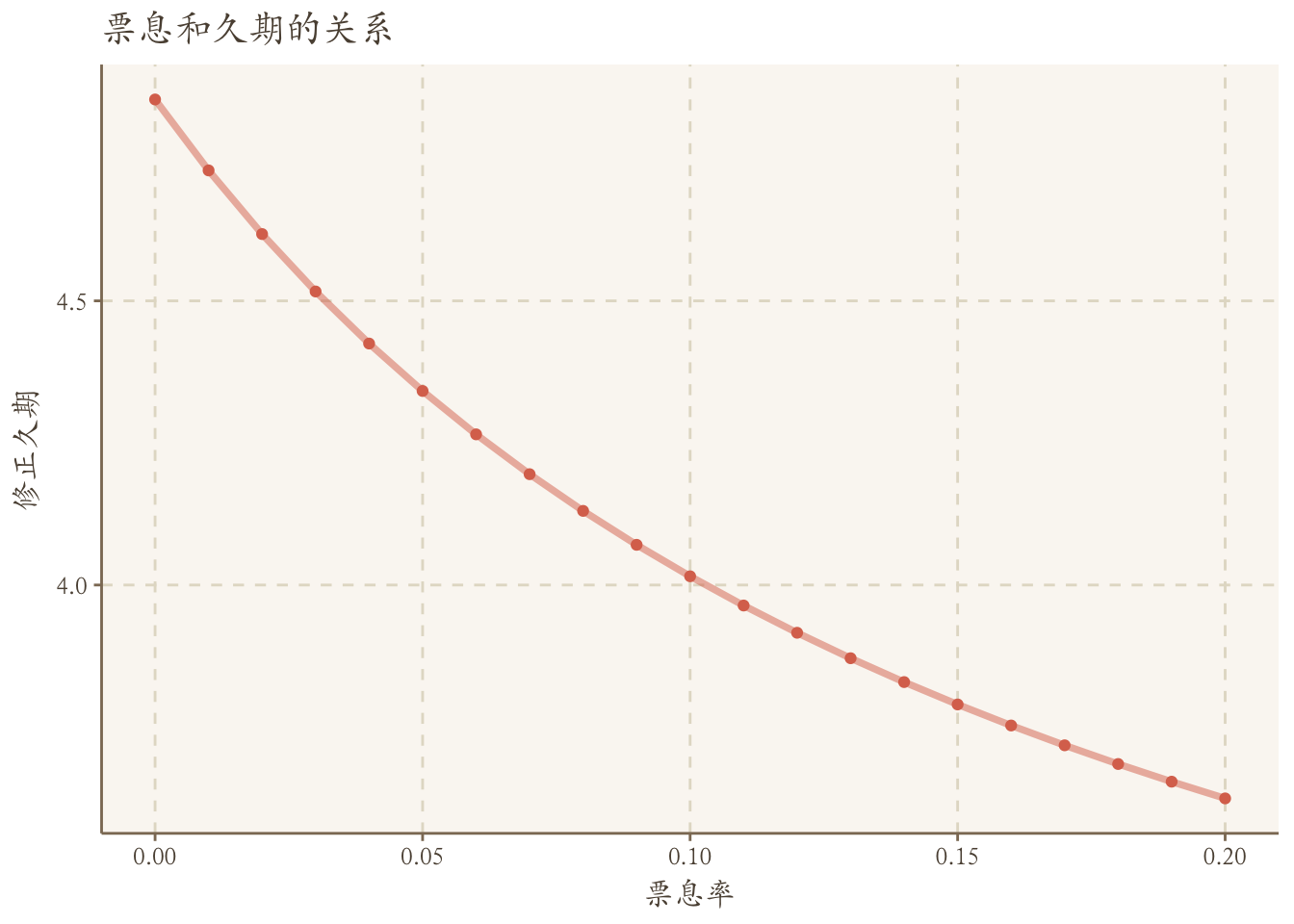
ggplot(df,aes(x=coup,y=sim_dur)) +
  geom_line(size=1.3,alpha=0.5)+geom_point()+
  ggtitle('票息和久期的关系') + xlab('票息率')+ylab('修正久期')+theme(text = element_text(family='Kai'))

使用JrvFiance包计算债券ytm

# yield参数结算日，到期日，票息率，当前价格
bond.yield(settle='2018-01-01', mature='2023-01-01', coupon=5e-2, price=101)
## [1] 0.04772823
#如果需要一次计算很多债券的ytm，可以参考下面的例子
bond.yields(settle="2012-01-01", mature=c("2022-01-01", "2032-01-01"),
            coupon=c(0.09, 0.08,0.07,0.06),
            price=c(94, 83, 81, 65))
## [1] 0.09961336 0.09978548 0.10056533 0.10110332