利率练习2

张剑

2020/03/16

Categories: 投资学 Tags: 投资

题目背景

你面临如下投资决策，现在支出70000万，投资期限为5年，每年的回报率为1万，现在的利率为5%，5年后投资结束，回收45000元，请问你是否应该参与这项投资？

#首先加载包
pacman::p_load(tidyverse,DT,ggforce,ggthemes)

#建立现金流
cf <- tribble(~year, ~cf,
              0,-70000,
              1,10000,
              2,10000,
              3,10000,
              4,10000,
              5,55000)
r <- 0.05
cf %>%
  mutate(pv =cf/(1+r)^year)  %>% 
  datatable(rownames = F,caption = '这项投资的现金流表',colnames = c('年份','现金流','现值'))
#计算npv
npv <- cf %>%
  mutate(pv =cf/(1+r)^year)  %>% 
  select(pv) %>%
  sum()
if (npv>0){
  paste("该项的npv为：",npv,',可行！')
}else {
  paste("该项的npv为：",npv,',不可行！')
}
## [1] "该项的npv为： 8553.44419738884 ,可行！"

真实利率计算，名义利率为4%，计算半年计息，月度计息的真实利率,我们知道有一个公式

(1+sr/n)n=1+r

其中sr为名义利率，n为计息周期，r为真实利率

我们演示一下如何自己写函数

s_r <- 0.04 #名义利率
n <- 2 # 计息周期
e_r_2 <- (1+s_r/n)^n-1 

# 那么我们可以自己写一个函数
myfun <- function(s_r , n) {
  e_r = (1+s_r/n)^n -1
  return(e_r)
}
#计算一个每月计息的名义利率的实际利率
myfun(0.5,12)
## [1] 0.6320941

接下来我们尝试考虑一下某些借款平台的日息万三的利率其实际利率是多少

(1+sr)360=1+r

myfun_2 <- function(sr,n) {
  return((1+sr)^n-1)
}
myfun_2 (0.0003,360)
## [1] 0.1140297

年金终值，现值，我们也可以依葫芦画瓢自己写函数，这里就不展示了

接下来一个分期付款的例子

车价150000

贷款100000

贷款利率6%年实际利率

五年还清，请问每月还多少？

library(FinCal)

#这个函数有以下参数 r对应期的贴现率，n期数，pv现值，fv终止，返还的是每期支付。
pmt(r=0.06/12,pv=-100000,n = 60,fv=0)
## [1] 1933.28

另一个简单的例子

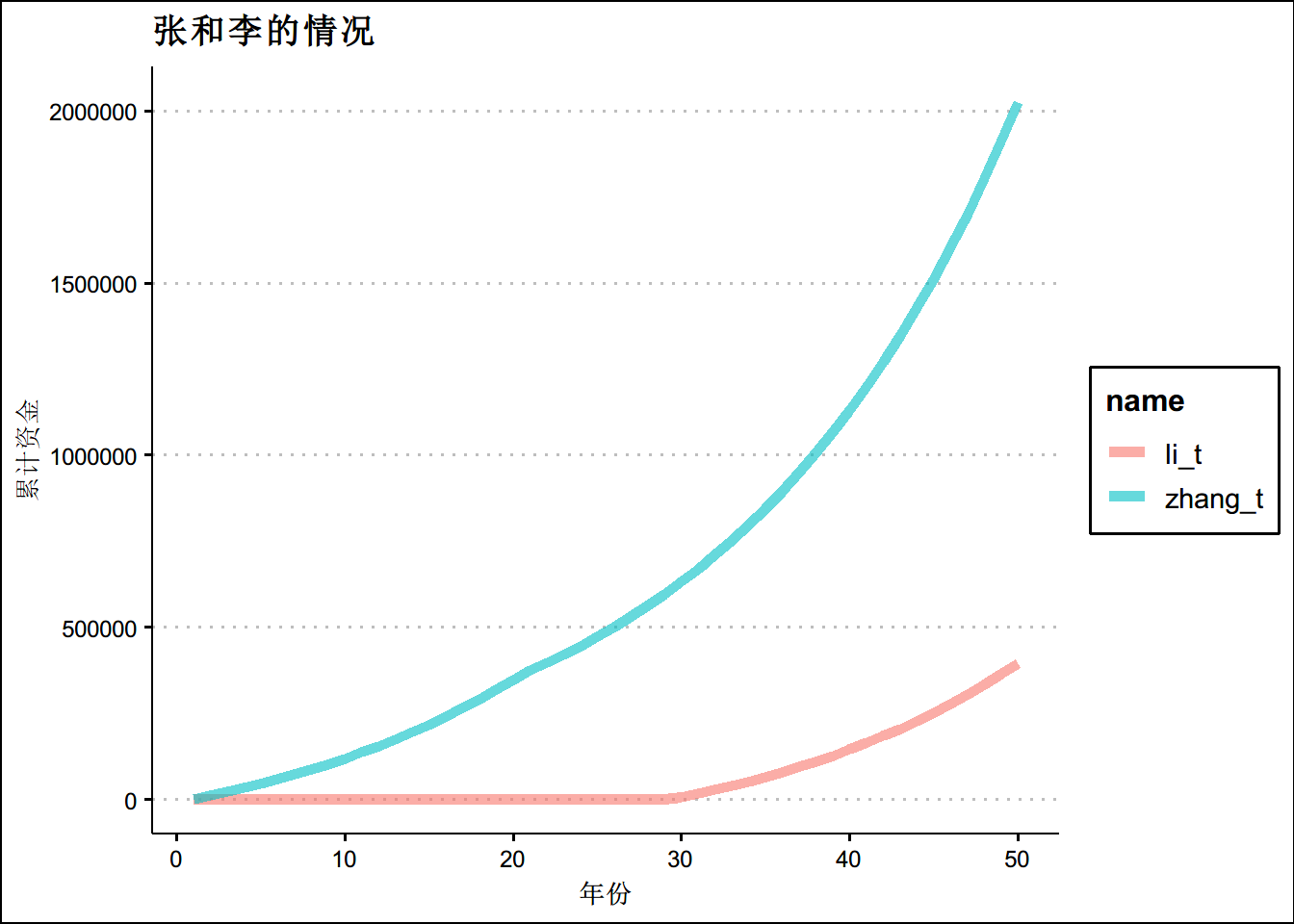
张和李两个年轻人，两人都是20岁，张决定20到40岁存钱，李决定50-70岁存钱，假设70岁退休，利率给定6%，展示两人的累计财富。

r <-0.06
cf <- tibble(period= 1:50,zhang=0,li=0,zhang_t=0,li_t=0)
cf <- cf %>%
  mutate(zhang=if_else(period %in% seq(1,20,by=1),5000,0)) %>%
  mutate(li = if_else(period %in% seq(30,50,by=1),5000,0))

for (i in 2:50) {
  cf[i,"zhang_t"] <- (cf[i-1,'zhang']+cf[i-1,'zhang_t'])*r + cf[i,"zhang"]+cf[i-1,'zhang_t']+cf[i-1,'zhang']
    cf[i,"li_t"] <- (cf[i-1,'li']+cf[i-1,'li_t'])*r + cf[i,"li"]+cf[i-1,'li_t']+cf[i-1,'li']
}

cf %>%
  datatable(rownames = F,colnames = c('年份','张每年存的钱','李每年存的钱','张的累计','李的累计'))
cf <- cf %>%
  select(period,zhang_t,li_t) %>%
  gather(key="name",value="value",-period)

myp <- ggplot(data = cf,mapping = aes(x=period,y=value,color=name))+
  geom_line(size=2,alpha=0.6)+
  theme_clean()+
  xlab("年份") +
  ylab('累计资金')+
  ggtitle("张和李的情况")
myp