投资决策之——内部收益率法则
IRR计算思路演示
这里我们只需使用tidyverse包绘图
pacman::p_load(tidyverse)
x <-c() # 建立两个空集,用于存储循环数据
y <-c()
for ( i in seq(0,0.2,by = 0.0001)){ # 建立for循环,起点终点步长
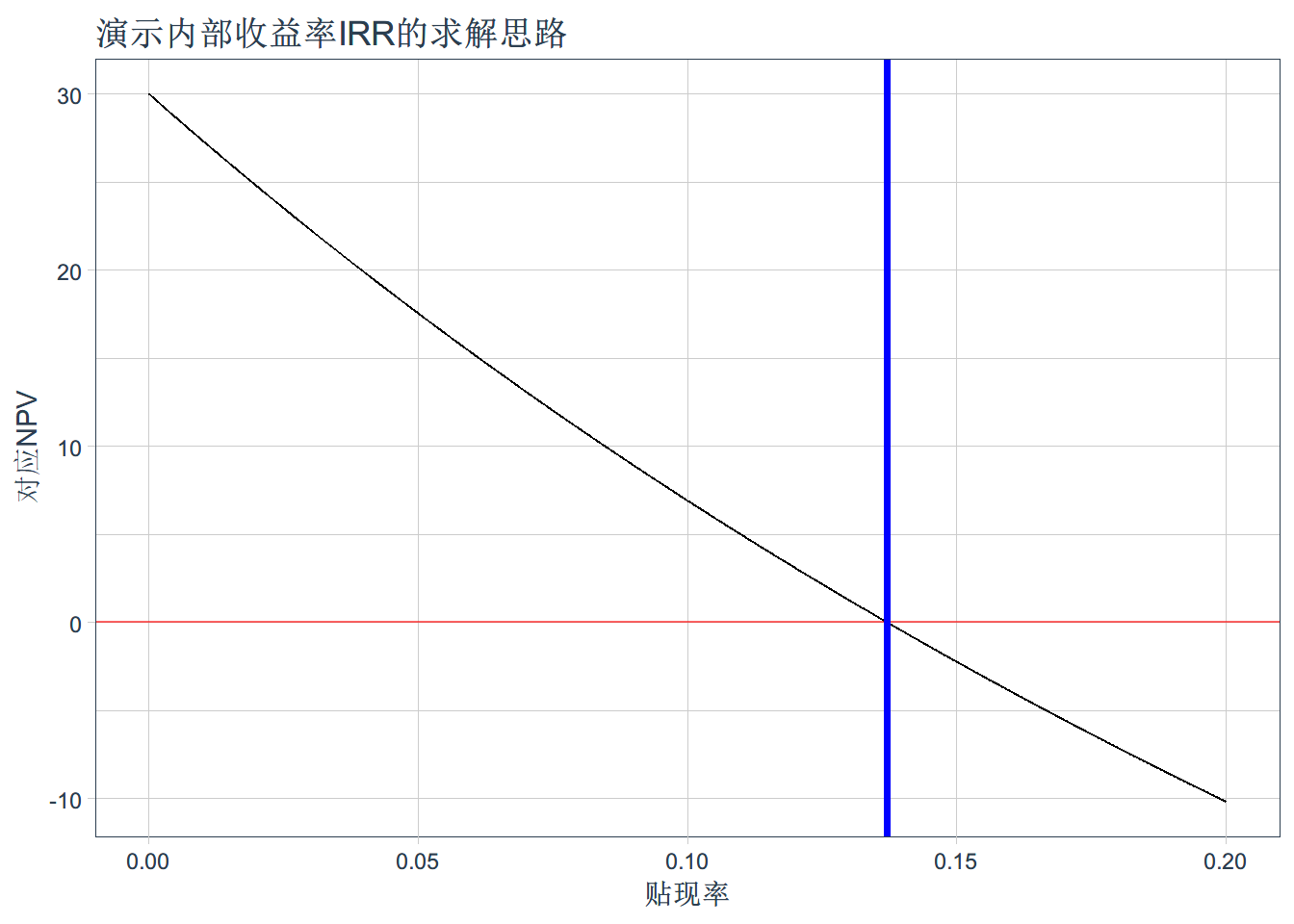
npv = -100+ 30/(1+i)+60/(1+i)^2+40/(1+i)^3
x = append(x,i)
y = append(y,npv)
}
res <- tibble(irr=x,npv=y) #将循环数据存储为数据集
#作图
ggplot(res,aes(x=irr,y=npv)) + geom_line()+
geom_hline(yintercept = 0 ,color='red',alpha=0.6) +
geom_vline(xintercept = 0.137,size=1.3,color='blue') +
tidyquant::theme_tq() + xlab('贴现率')+ylab('对应NPV') +
ggtitle('演示内部收益率IRR的求解思路')## Registered S3 method overwritten by 'quantmod':
## method from
## as.zoo.data.frame zoo支付宝借呗内部收益率计算
R之所以强大是因为用的人多,包多。我们这里调用jrvFinancez这个包来帮助我们直接计算irr
pacman::p_load(jrvFinance,tidyverse,DT)
cf <- tibble(cf=c(-50000,190,310,300,310,310,300,
310,300,310,310,280,50310),t=seq(0:12))
cf %>% datatable()xlhb_irr <- irr(cf$cf,cf.freq = 12)
paste('先利后本的IRR是',xlhb_irr)## [1] "先利后本的IRR是 0.0730734556310215"那么先利后本的还款方式的IRR是7.31%
接下来我们计算每月等额的IRR
cf_2 <- tibble(cf = c(-50000,rep(4324.16,12)),t=seq(0,12))
cf_2 %>% datatable()myde_irr <- irr(cf_2$cf,cf.freq = 12)
paste('每月等额的IRR是',xlhb_irr)## [1] "每月等额的IRR是 0.0730734556310215"那么先利后本的还款方式的IRR是7.13%,和先利后本的差距不到0.2%
接下来可结合其他信贷产品,考虑借款便利性与承受能力确定是否选择使用借呗借款,以及选择何种方式借款。
纯储蓄(投资型)保险是否值得购买
# 该保险现金流分布
cf <- tibble(period= 0:65,exp = 0)
cf <- cf %>%
mutate(exp = if_else(period %in% seq(0,9),-6000,0)) %>%
mutate(income = if_else(period %in% seq(3,65,by = 2),3000,0))
cf[66,"income"] <- 300000
#上一行是为最后一期赋值
#展示一下现金流
cf<-cf %>% mutate(pmt = exp+income) %>%
mutate(cum = cumsum(pmt))
cf %>% datatable(rownames = F, caption = "该保险的现金流",
colnames = c('年份','支出','收益','净收益','累计收益'))#计算净收益的irr
irr <- cf %>%
select(pmt) %>%
pull() %>%
irr()
#利用jrv包进行计算,注意40行用了一个pull函数
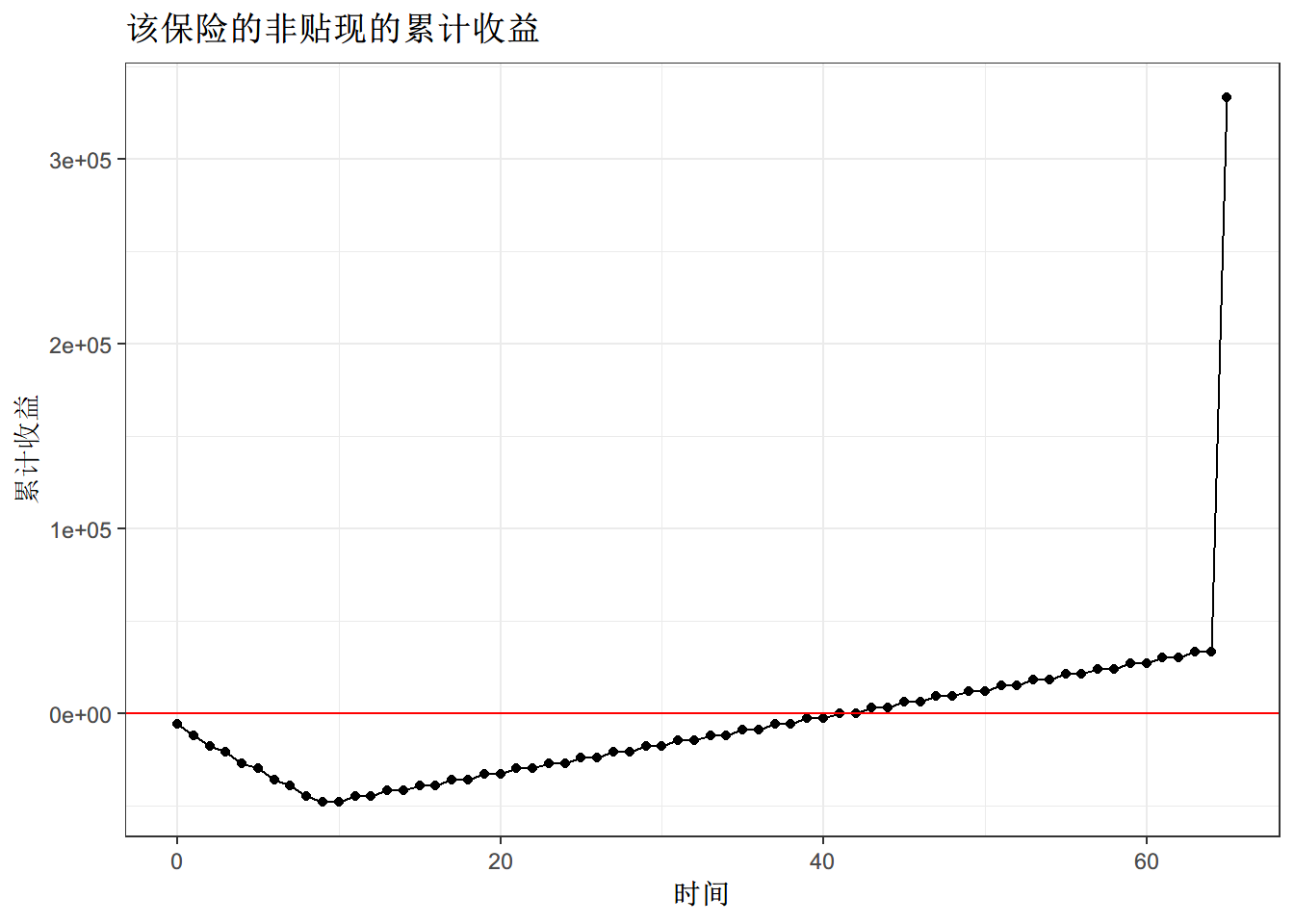
paste("该保险产品的IRR是:",irr)## [1] "该保险产品的IRR是: 0.0428546906155038"ggplot(cf,aes(x=period,y=cum))+geom_point()+
geom_line()+theme_bw()+geom_hline(yintercept = 0,color='red')+
xlab('时间')+ylab('累计收益')+ggtitle('该保险的非贴现的累计收益')那么这项保险产品的现金流的IRR不到5%左右,是否值得选择呢?需要结合投资者面临的投资环境综合分析。
最后补充一个小小的内容:
在R中使用for循环是非常慢的,一般不要大量使用for循环,比如我们前面用for循环来演示irr求解的时候,如果把步长设置的较小,会导致运算速度很慢,这时建议大家使用apply函数,会大幅提升运算性能。
具体演示如下:
pacman::p_load(microbenchmark)
fun1 <- function(){
x <-c()
y <-c()
for ( i in seq(0,0.2,by = 0.0001)){
npv = -100+ 30/(1+i)+60/(1+i)^2+40/(1+i)^3
x = append(x,i)
y = append(y,npv)
}
res <- tibble(irr=x,npv=y)
return(res)
}
fun2<-function(){
irr <-seq(0,0.2,by=0.0001)
myfun <- function(i){
npv = -100+ 30/(1+i)+60/(1+i)^2+40/(1+i)^3
}
npv <- sapply(irr,myfun)
res <- tibble(irr=irr,npv=npv)
return(res)
}
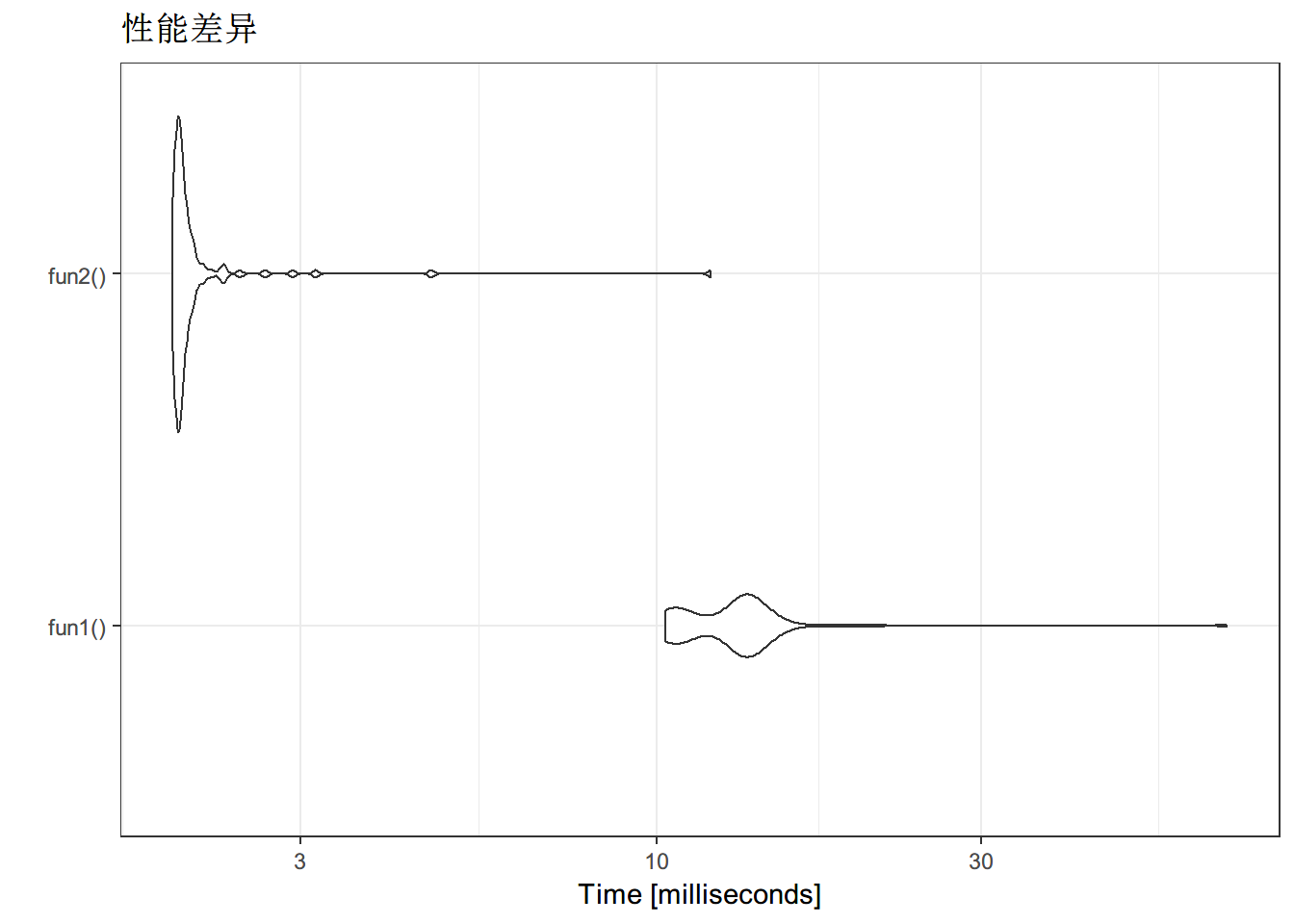
res<-microbenchmark(fun1(),fun2())
res## Unit: milliseconds
## expr min lq mean median uq max neval cld
## fun1() 10.3038 10.8384 13.32147 13.3481 13.66435 68.9810 100 b
## fun2() 1.9464 1.9748 2.17579 1.9983 2.05075 12.0258 100 aautoplot(res) + theme_bw() + ggtitle('性能差异')## Coordinate system already present. Adding new coordinate system, which will replace the existing one.